第三章《不等式》复习测试题(二)
三、解答题
12.某商场计划出售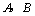 两种商品,商场根据实际情况和市场需求,得到如下数据:(商品单位:件) 两种商品,商场根据实际情况和市场需求,得到如下数据:(商品单位:件)
资金(百元)
|
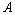 商品 商品
|
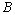 商品 商品
|
日资金供应量
|
单位进价
|
30
|
20
|
3000
|
单位工资支出
|
5
|
10
|
1100
|
单位利润
|
6
|
8
|
|
问如何确定两种货物的月供应量,可以使得总利润达到最大?最大利润为多少?
考查目的:考查二元一次不等式组表示的平面区域、线性规划问题等基础知识和方法,考查数形结合能力和应用数学知识解决实际问题的能力.
答案:40,90;960.
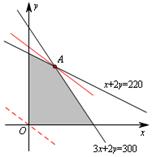
解析:设供应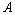 商品 商品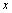 件, 件,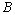 商品 商品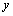 件,总利润为 件,总利润为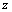 百元,则 百元,则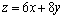 ,根据题意得约束条件为 ,根据题意得约束条件为 ,即 ,即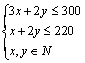 .作出可行域如图所示.目标函数 .作出可行域如图所示.目标函数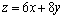 表示一组斜率为 表示一组斜率为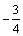 的平行直线,其在 的平行直线,其在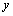 轴上的截距为 轴上的截距为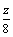 .由图可知,当直线 .由图可知,当直线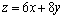 经过点 经过点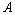 (即直线 (即直线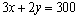 与 与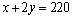 的交点)时直线在 的交点)时直线在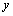 轴上的截距最大,此时 轴上的截距最大,此时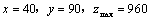 . .
13.(2007江西理)已知函数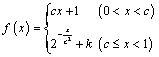 在区间 在区间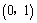 内连续,且 内连续,且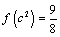 . .
⑴求实数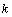 和 和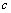 的值; 的值;
⑵解不等式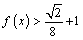 . .
考查目的:考查分段函数、连续函数的概念等基础知识,考查不等式的解法以及综合运用知识解决问题的能力.
答案:⑴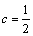 , ,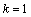 ;⑵ ;⑵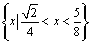 . .
解析:⑴∵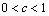 ,∴ ,∴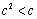 .由 .由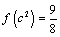 ,即 ,即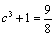 ,得 ,得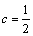 ,∴ ,∴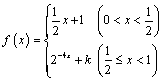 . 又∵ . 又∵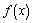 在 在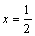 处连续,∴ 处连续,∴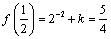 ,解得 ,解得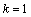 . .
⑵由⑴得,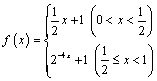 . 由 . 由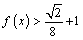 得,当 得,当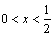 时,解得 时,解得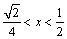 ;当 ;当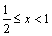 时,解得 时,解得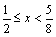 ,∴不等式 ,∴不等式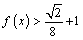 的解集为 的解集为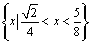 . .
14.(2011安徽理)⑴设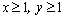 ,证明: ,证明: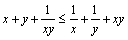 ; ;
⑵设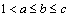 ,证明: ,证明: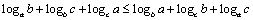 . .
考查目的:考查不等式的基本性质、对数函数的性质和对数换底公式等基本知识,考查不等式证明的基本方法,以及代数式的恒等变形能力和推理论证能力.
解析:证明:⑴∵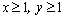 ,∴要证原不等式成立,只需证明 ,∴要证原不等式成立,只需证明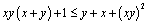 .由于 .由于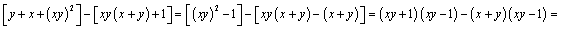
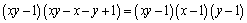 ,而 ,而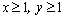 ,∴ ,∴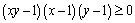 ,从而所要证明的不等式成立. ,从而所要证明的不等式成立.
⑵设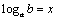 , ,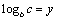 ,由对数换底公式得 ,由对数换底公式得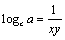 , ,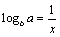 , ,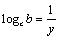 , ,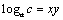 ,于是,所要证明的不等式即为 ,于是,所要证明的不等式即为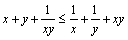 .∵ .∵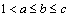 ,∴ ,∴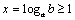 , ,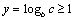 ,∴由⑴可知所要证明的不等式成立. ,∴由⑴可知所要证明的不等式成立.
15.(2009江苏)按照某学者的理论,假设一个人生产某产品单件成本为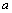 元,如果他卖出该产品的单价为 元,如果他卖出该产品的单价为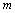 元,则他的满意度为 元,则他的满意度为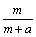 ;如果他买进该产品的单价为 ;如果他买进该产品的单价为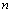 元,则他的满意度为 元,则他的满意度为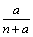 .如果一个人对两种交易(卖出或买进)的满意度分别为 .如果一个人对两种交易(卖出或买进)的满意度分别为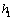 和 和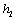 ,则他对这两种交易的综合满意度为 ,则他对这两种交易的综合满意度为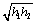 . .
现假设甲生产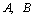 两种产品的单件成本分别为12元和5元,乙生产 两种产品的单件成本分别为12元和5元,乙生产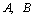 两种产品的单件成本分别为3元和20元,设产品 两种产品的单件成本分别为3元和20元,设产品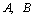 的单价分别为 的单价分别为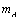 元和 元和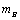 元,甲买进 元,甲买进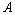 与卖出 与卖出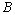 的综合满意度为 的综合满意度为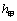 ,乙卖出 ,乙卖出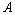 与买进 与买进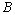 的综合满意度为 的综合满意度为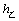 . .
⑴求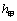 和 和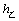 关于 关于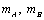 的表达式;当 的表达式;当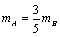 时,求证: 时,求证: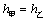 ; ;
⑵设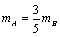 ,当 ,当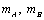 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少? 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
⑶记⑵中最大的综合满意度为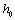 ,试问能否适当选取 ,试问能否适当选取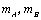 的值,使得 的值,使得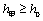 和 和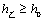 同时成立,但等号不同时成立?试说明理由. 同时成立,但等号不同时成立?试说明理由.
考查目的:考查函数的概念、基本不等式等基础知识,考查数学建模能力、抽象概括能力、数学阅读理解能力以及运算求解能力.
答案:⑴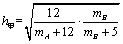 , ,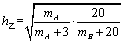 ;⑵当 ;⑵当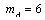 , ,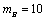 时,甲乙两人同时取到最大的综合满意度为 时,甲乙两人同时取到最大的综合满意度为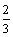 ;⑶不能. ;⑶不能.
解析:⑴根据题意,甲买进产品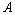 的满意度 的满意度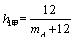 ,甲卖出产品 ,甲卖出产品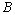 的满意度 的满意度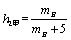 ,∴甲买进 ,∴甲买进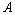 与卖出 与卖出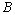 的综合满意度为 的综合满意度为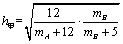 ;同理,乙卖出 ;同理,乙卖出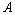 与买进 与买进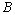 的综合满意度为 的综合满意度为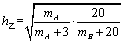 . .
当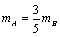 时, 时,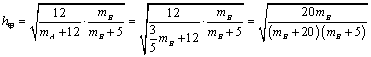 , ,
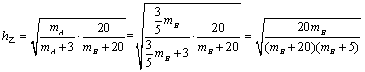 ,∴ ,∴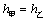  . .
⑵设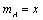 , ,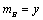 .由⑴知,当 .由⑴知,当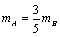 ,即 ,即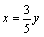 时, 时,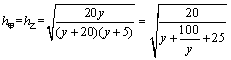 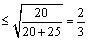 ,当且仅当 ,当且仅当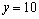 时取等号,此时 时取等号,此时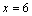 ,∴当 ,∴当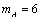 , ,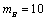 时,甲、乙两人的综合满意度均最大,且最大的综合满意度为 时,甲、乙两人的综合满意度均最大,且最大的综合满意度为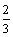 . .
⑶由⑵知,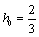 ,∵ ,∵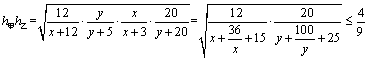 ,∴当 ,∴当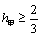 , ,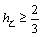 时,有 时,有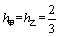 ,因此不能取到 ,因此不能取到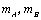 的值,使得 的值,使得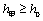 和 和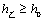 同时成立,但等号不同时成立. 同时成立,但等号不同时成立.
(责任编辑:admin)
|
 ,即
,即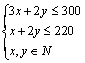 .作出可行域如图所示.目标函数
.作出可行域如图所示.目标函数
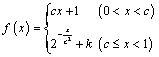 在区间
在区间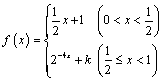 . 又∵
. 又∵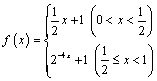 . 由
. 由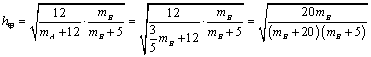 ,
,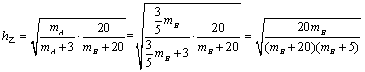 ,∴
,∴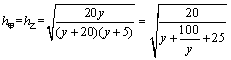
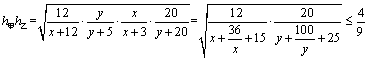 ,∴当
,∴当