《1.2 应用举例(1)》测试题
一、选择题
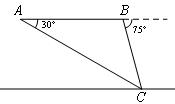
1.飞机沿水平方向飞行,在 处测得正前下方地面目标 处测得正前下方地面目标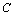 的俯角为 的俯角为 ,向前飞行 ,向前飞行 米,到达 米,到达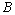 处,此时测得目标 处,此时测得目标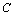 的俯角为 的俯角为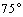 ,这时飞机与地面目标的直线距离为( ). ,这时飞机与地面目标的直线距离为( ).
A.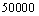 米 B. 米 B.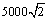 米 C. 米 C.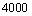 米 D. 米 D.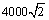 米 米
考查目的:考查正弦定理的应用.
答案:B.
解析:如图,在 中,根据正弦定理得 中,根据正弦定理得 ,解得 ,解得 (米). (米).
2.某人向正东方向走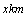 ,然后右转 ,然后右转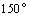 ,朝前走 ,朝前走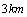 ,结果他离出发点恰好 ,结果他离出发点恰好 ,则 ,则 的值为( ). 的值为( ).
A.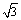 B. B. C. C.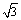 或 或 D. D.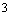
考查目的:考查余弦定理、方程思想.
答案:C.
解析:根据余弦定理得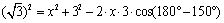 ,化简并整理得 ,化简并整理得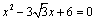 ,解得 ,解得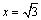 或 或 . .
3. (由2010浙江文改编)在 中,角 中,角 所对的边分别为 所对的边分别为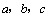 ,设 ,设 为 为 的面积,满足 的面积,满足 ,则角 ,则角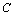 的大小为( ). 的大小为( ).
A.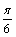 B. B. C. C.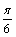 或 或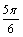 D. D. 或 或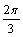
考查目的:考查余弦定理、三角形面积公式、三角变换等基础知识.
答案:B
解析:∵ ,∴根据余弦定理和三角形面积公式得 ,∴根据余弦定理和三角形面积公式得 ,∴ ,∴ , ,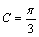 . .
二、填空题
4.(2008江苏卷)在 中,若 中,若 , ,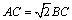 ,则 ,则 的最大值是 . 的最大值是 .
考查目的:考查三角形面积公式、余弦定理以及函数思想.
答案: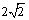 . .
解析:设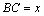 ,则 ,则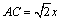 ,根据面积公式得 ,根据面积公式得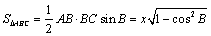 ;根据余弦定理得 ;根据余弦定理得 ,∴ ,∴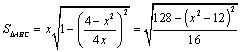 , ,
由三角形三边关系有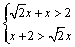 ,解得 ,解得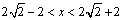 ,故当 ,故当 时, 时, 取得最大值 取得最大值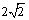 . .
5.(2011安徽理)已知 的一个内角为 的一个内角为 ,并且三边长构成公差为4的等差数列,则 ,并且三边长构成公差为4的等差数列,则 的面积为_______________. 的面积为_______________.
考查目的:考查余弦定理、等差数列的概念及三角形面积公式.
答案: . .
解析:根据题意,可设 的三边长分别为 的三边长分别为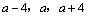 ,由 ,由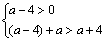 得 得 .由余弦定理得 .由余弦定理得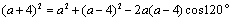 ,解得 ,解得 ( (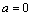 舍去),∴ 舍去),∴
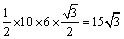 . .
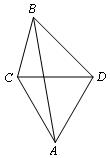
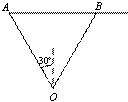
6.如图,某炮兵阵地位于 点,两观察所位于 点,两观察所位于 两点,已知 两点,已知 为正三角形,且 为正三角形,且 ,当目标出现在 ,当目标出现在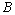 时,测得 时,测得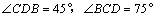 ,则炮兵阵地与目标的距离约为 (精确到 ,则炮兵阵地与目标的距离约为 (精确到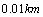 ). ).
考查目的:考查利用正弦定理、余弦定理解决实际问题的能力.
答案: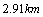 . .
解析:如图, ,在 ,在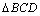 中,由正弦定理得 中,由正弦定理得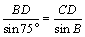 ,∴ ,∴ .在 .在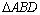 中, 中,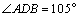 ,由余弦定理得 ,由余弦定理得  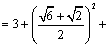
 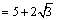 ,∴ ,∴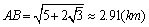 . .
三、解答题:
7.(2007海南、宁夏)如图,测量河对岸的塔高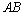 时,可以选与塔底 时,可以选与塔底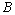 在同一水平面内的两个侧点 在同一水平面内的两个侧点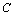 与 与 .现测得 .现测得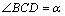 , ,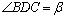 , ,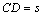 并在点 并在点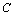 测得塔顶 测得塔顶 的仰角为 的仰角为 ,求塔高 ,求塔高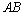 . .
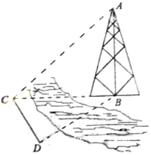
考查目的:考查正弦定理、直角三角形的边角关系以及空间想象能力和运算求解能力.
答案: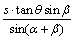 . .
解析:在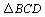 中, 中,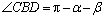 .由正弦定理得 .由正弦定理得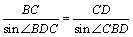 ,∴ ,∴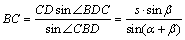 .在 .在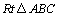 中, 中, . .
8.(2010福建理)某港口 要将一件重要物品用小艇送到一艘正在航行的轮船上. 在小艇出发时,轮船位于港口 要将一件重要物品用小艇送到一艘正在航行的轮船上. 在小艇出发时,轮船位于港口 北偏西 北偏西 且与该港口相距 且与该港口相距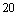 海里的 海里的 处,并以 处,并以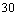 海里/小时的航行速度沿正东方向匀速行驶. 假设该小船沿直线方向以 海里/小时的航行速度沿正东方向匀速行驶. 假设该小船沿直线方向以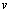 海里/小时的航行速度匀速行驶,经过 海里/小时的航行速度匀速行驶,经过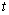 小时与轮船相遇. 小时与轮船相遇.
⑴若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
⑵假设小艇的最高航行速度只能达到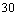 海里/小时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由. 海里/小时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
考查目的:考查利用直角三角形的边角关系、余弦定理解三角形,以及综合运用知识分析问题解决问题的能力.
答案:⑴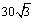 海里/小时,⑵航行方向是北偏东 海里/小时,⑵航行方向是北偏东 ,航行速度为 ,航行速度为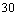 海里/小时. 海里/小时.
解析:(方法一)⑴设相遇时小艇航行的距离为 海里,则 海里,则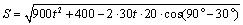 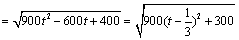 ,∴当 ,∴当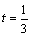 时, 时, ,此时 ,此时 ,即小艇以 ,即小艇以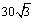 海里/小时的速度航行,相遇时小艇的航行距离最小. 海里/小时的速度航行,相遇时小艇的航行距离最小.
⑵设小艇与轮船在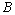 处相遇,则 处相遇,则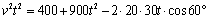 ,∴ ,∴ . ∵ . ∵ ,∴ ,∴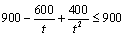 ,即 ,即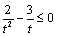 ,解得 ,解得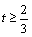 .又∵ .又∵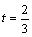 时, 时,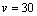 ,故 ,故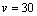 时, 时,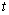 取得最小值,且最小值等于 取得最小值,且最小值等于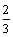 . .
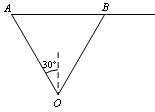
此时,在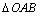 中,有 中,有 ,故可设计航行方案如下:航行方向是北偏东 ,故可设计航行方案如下:航行方向是北偏东 ,航行速度为 ,航行速度为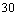 海里/小时,这样,小艇能以最短时间与轮船相遇. 海里/小时,这样,小艇能以最短时间与轮船相遇.
(方法二)⑴若相遇时小艇的航行距离最小,又轮船沿正东方向匀速行驶,则小艇航行方向为正北方向,设小艇与轮船在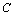 处相遇. 在 处相遇. 在 中, 中, , , ;又 ;又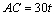 , ,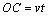 ,此时,轮船航行时间 ,此时,轮船航行时间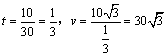 ,即小艇以 ,即小艇以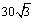 海里/小时的速度航行,相遇时小艇的航行距离最小. 海里/小时的速度航行,相遇时小艇的航行距离最小.
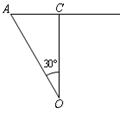
⑵猜想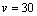 时,小艇能以最短时间与轮船在 时,小艇能以最短时间与轮船在 处相遇,此时 处相遇,此时 .又∵ .又∵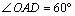 ,∴ ,∴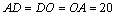 ,解得 ,解得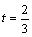 . .
据此可设计航行方案如下:航行方向为北偏东 ,航行速度的大小为 ,航行速度的大小为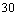 海里/小时,这样,小艇能以最短时间与轮船相遇. 证明如下: 海里/小时,这样,小艇能以最短时间与轮船相遇. 证明如下:

如图,由⑴得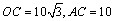 ,故 ,故 ,且对于线段 ,且对于线段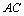 上任意点 上任意点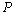 ,有 ,有 . 而小艇的最高航行速度只能达到 . 而小艇的最高航行速度只能达到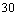 海里/小时,故小艇与轮船不可能在 海里/小时,故小艇与轮船不可能在 , ,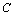 之间(包含 之间(包含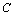 )的任意位置相遇. )的任意位置相遇.
设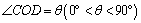 ,则在 ,则在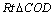 中, 中,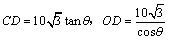 .由于从出 .由于从出 发到相遇,轮船与小艇所需要的时间分别为 发到相遇,轮船与小艇所需要的时间分别为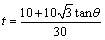 和 和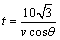 ,∴ ,∴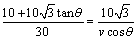 ,由此可得, ,由此可得,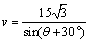 .又∵ .又∵ ,∴ ,∴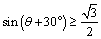 ,从而 ,从而 ,由于 ,由于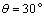 时, 时, 取得最小值 取得最小值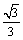 ,于是当 ,于是当 时, 时,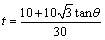 取得最小值,且最小值为 取得最小值,且最小值为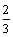 ,故可设计航行方案如下:航行方向为北偏东 ,故可设计航行方案如下:航行方向为北偏东 ,航行速度为 ,航行速度为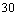 海里/小时,小艇能以最短时间与轮船相遇. 海里/小时,小艇能以最短时间与轮船相遇.
(方法三)⑴同方法一或方法二.
⑵ 设小艇与轮船在 设小艇与轮船在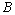 处相遇,依题意得 处相遇,依题意得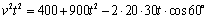 ,∴ ,∴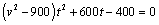 . .
(i)若 ,则由 ,则由 得, 得,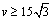 ,∴ ,∴ .①当 .①当 时,令 时,令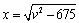 ,则 ,则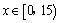 , ,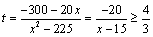 ,当且仅当 ,当且仅当 即 即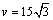 时等号成立. 时等号成立.
②当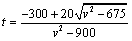 时,同理可得 时,同理可得 . 由①②得,当 . 由①②得,当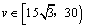 时, 时,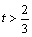 . .
(ii)若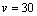 ,则 ,则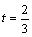 . .
综合(i)(ii)可知,当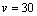 时, 时,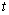 取最小值 取最小值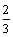 ,此时,在 ,此时,在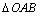 中, 中, ,故可设计航行方案如下:航行方向为北偏东 ,故可设计航行方案如下:航行方向为北偏东 ,航行速度为 ,航行速度为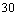 海里/小时,小艇能以最短时间与轮船相遇. 海里/小时,小艇能以最短时间与轮船相遇.
(责任编辑:admin)
|

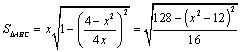 ,
,


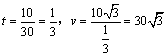 ,即小艇以
,即小艇以

