一道三角题的多种解法与“弦图”背景
http://www.newdu.com 2025/05/19 07:05:42 人民教育出版社 佚名 参加讨论
一道三角题的多种解法与“弦图”背景 湖北省阳新县高级中学 邹生书 题目 以  的斜边 为一边向形外作正方形 ，设 ，求证: .这是笔者从华中师范大学彭翕成老师的博客中看到的一道题目，该题首先是由彭老师发给史嘉老师的并且要求用向量进行解答，然后史嘉老师将此题发到人教网上征求解答，引起网友们的强烈反响和热烈参与，解法多种多样精彩纷呈，笔者从中受益匪浅，现将有关解法和本人的肤浅体会整理成文与大家分享. 一、路漫漫其修远兮，吾将上下而求索 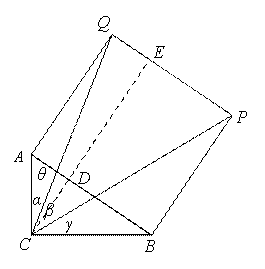 图1 证法1 如图1，过点 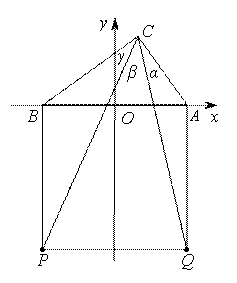 作 于点 交于点 ，设 ，设正方形的边长为1，则 ， ， .于是   .同理 ， .由余弦定理得， ， ，  图2  .由上易证 .证法2 以 的中点 为坐标原点建立直角坐标系如图2所示，设正方形的边长为2.依题意点在以为直径的上半圆上，设点的坐标为 .由向量夹角公式知，要证.只要证 ，只要证 . 由  ，得 .由 ， ，得  .所以  .又  ， ， .所以  ，所以 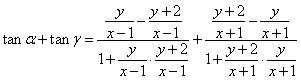，故.证法3以 的中点为坐标原点建立直角坐标系如图2所示，设正方形的边长为2，依题意点在以为直径的上半圆上，设点的坐标为 .因为  ，所以要证，只要证 ，即要证 ，两边同除以 ，则只要证 .由到角公式得，   .故 .二、“弦图”背景——会当临绝顶，一览众山小 该题文字简洁解法多样且背景深厚.上述证法运算量较大，若将其补成一个正方形如图3所示，补形后不仅图形对称完美，而且证明思路更加清晰证法更加简洁直观. 证法4 同法2只要证 .如图3，过点 作 交 的延长线于点 ，过点 作 交 的延长线于点 ，设直线 图3  相交于点 ，易证四边形 是正方形，且四个角上的四个直角形全等，此图就是我国古代数 学家赵爽用于证明勾股定理的“弦图”. 设  ，则 ，则 .由向量数量积的几何意义得，  ， ，所以  .  .所以  .所以.故 .证法5 同法4补形成正方形，由直角三角形的边角关系得，  ，所以 .由余弦定理得， .综上 .证法6 如图3，因为 ，所以要证，只要证，即要证.而  ， ，所以，故 .证法7 同法6只要证 ，两边同除以，则只要证，而 ，故. 赵爽弦图 2002年国际数学家大会在北京召开，大会的会标是我国古代数学家赵爽画的“弦图”，体现了数学研究中的继承和发展.赵爽的“弦图”隐含了勾股定理的两种面积证法，其证法如下: 证法1 由“弦图”知，边长为  的正方形面积等于边长为 的正方形面积减去4个两直角边为 的三角形面积，即 .证法2由“弦图”知，边长为 的正方形面积等于边长为 的正方形面积加上4个两直角边为的三角形面积，即. 赵爽的“弦图”证法优美精巧是证明勾股定理最著名的证法之一，特别是“弦图”一图蕴涵两种证法更是举世无双.“弦图”是证明勾股定理的无字证明，充分体现了我国古代的数学文明和数学文化，本题补形后的“弦图”不仅图形对称完美，而且证明思路更加清晰证法更加简洁直观，使我们再次领会到“弦图”的魅力和丰富的数学内涵. (责任编辑：admin) |
- 上一篇：错解剖析得真知（三十三）
- 下一篇：高一数学答题技巧解题方法汇总（不断更新中）