错解剖析得真知（三十四）
http://www.newdu.com 2025/05/19 09:05:57 人民教育出版社 佚名 参加讨论
错解剖析得真知（三十四） §11.2 复数的运算 一、知识导学 1.复数加、减法的几何意义 (1)加法的几何意义 复数  是以 、 为两邻边的平行四边形对角线 所对应的复数.(2)复数减法的几何意义 复数  是连接向量 、 的终点，并指向被减数的向量 所对应的复数.2. 重要结论 （1） 对复数z 、  、 和自然数m、n，有 ， ， (2)  ， ， ， ； ， ， ， .(3)  ，  ， .(4)设  ， ， ， ， ， 二、疑难知识导析 1.对于  ，是复数运算与实数运算相互转化的主要依据，也是把复数看作整体进行运算的主要依据，在解题中加以认识并逐渐体会.2.在进行复数的运算时，不能把实数的某些法则和性质照搬到复数集中来，如下面的结论. 当  时，不总是成立的.(1)  ；(2)  ；(3)  ；(4)  ；(5)  三、经典例题导讲 [例1] 满足条件  的点的轨迹是（ ）A.椭圆 B.直线 C.线段 D.圆 错解：选A或B. 错因：如果把  看作动点Z到定点（0，2）的距离，由上式表示到两个定点（0，2）与（-1，0）的距离之和为常数  动点的轨迹符合椭圆的定义，但是，有一定的前提的就是两点间的距离小于定常数.正解：  点（0，2）与（-1，0）间的距离为，动点在两定点（0，-2）与（-1，0）之间，选C评注：加强对概念的理解加深，认真审题. [例2] 求值：  错解：原式=    错因：上面的解答错在没有真正理解  的含义，只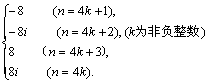是用了三个特殊整数代替了所有整数，犯了用特殊代替一般的错误.另外还可以看出对虚数单位 的整数幂的运算不熟悉，没有掌握虚数单位整数幂的运算结果的周期性.正解：原式=  =  =  评注：虚数单位 整数幂的值具有以4为周期的特点，根据 必须按被4整除余数为0、1、2、3四种情况进行分类讨论.[例3]已知  ，求 的值.分析：结论是等比数列的求和问题，所以应联想到求和公式  ，若直接将条件代入求和公式，则显得较为麻烦，不妨先将条件化简. 原式=  评注：由于数列中的数可以是复数，所以数列的诸性质在复数集中仍成立. [例4] （06年上海春卷）已知复数  满足 为虚数单位）， ，求一个以 为根的实系数一元二次方程.解法一：  ，  . 若实系数一元二次方程有虚根  ，则必有共轭虚根 .  ， 所求的一个一元二次方程可以是 . 解法二：设    ，得    ， 以下解法同解法一. [例5]   解析          四、典型习题导练 1．（06年四川卷）非空集合  关于运算 满足：（1）对任意 ，都有 ； （2）存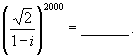在  ，使得对一切 ，都有 ，则称关于运算为“融洽集”；现给出下列集合和运算：①  ②  ③  ④  ⑤  其中 关于运算为“融洽集”__________;（写出所有“融洽集”的序号）2.  3．计算  4.计算  5．解下列方程： (1)  ；(2)  . (责任编辑：admin) |
- 上一篇：有心曲线直径三角形的一个性质及应用
- 下一篇：错解剖析得真知（三十三）