高中学习网-人民教育出版社人教版部编同步解析与测评答案-电子课本资料下载-知识点学习方法与技巧补课解题技巧学习计划表总结-人教网-高中试卷网题库网-中学学科网

首页 > 高中数学A版 > 解题技巧 >

错解剖析得真知（三十八）

http://www.newdu.com 2025/05/19 06:05:24 人民教育出版社 佚名 参加讨论


    错解剖析得真知（三十八）
    第十三章 算法初步
    §13.1 流程图
    一、 知识导学
    1.       流程图：是由一些图框和带箭头的流线组成的，其中图框表示各种操作的类型，图框中的文字和符号表示操作的内容，带箭头的流线表示操作的先后次序.
    2．算法的三种基本的逻辑结构：顺序结构、条件结构、循环结构.
    3．根据对条件的不同处理，循环结构又分为两种：
    直到型(until型)循环：在执行了一次循环体之后，对控制循环条件进行判断，当条件不满足时执行循环体.满足则停止.如图13-1-3，先执行A框，再判断给定的条件是否为“假”，若为“假”，则再执行A，如此反复，直到为“真”为止.
    当型（while型）循环：在每次执行循环体前对控制循环条件进行判断，当条件满足时执行循环体，不满足则停止.如图13-1-4，当给定的条件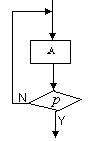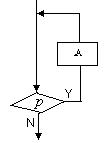成立（“真”）时，反复执行A框操作，直到条件为“假”时才停止循环.
                  
                       图13-1-1                      图13-1-2
    二、疑难知识导析
    1.“算法“没有一个精确化的定义，教科书只对它作了描述性说明，算法具有如下特点：
    （1）有限性：一个算法的步骤是有限的，必须在有限操作之后停止，不能是无限的.
    （2）确定性：算法的每一步骤和次序应当是确定的.
    （3）有效性：算法的每一步骤都必须是有效的.
    2. 画流程图时必须注意以下几方面：
    （1）使用标准的图形符号.
    （2）流程图一般按从上到下、从左到右的方向画.
    （3）除判断框外，大多数流程图符号只有一个进入点和一个退出点.判断框具有超过一个退出点的唯一符号.
    （4）判断框分两大类，一类判断框“是”与“否”两分支的判断，而且有且仅有两个结果；另一类是多分支判断，有几种不同的结果.
    （5）在图形符号内描述的语言要非常简练清楚.
    3. 算法三种逻辑结构的几点说明：
    （1）顺序结构是最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的.在流程图中的体现就是用流程线自上而下地连接起来，按顺序执行算法步骤.（2）一个条件结构可以有多个判断框.
    （3）循环结构要在某个条件下终止循环，这就需要条件结构来判断.在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数，累加变量用语输出结果，计数变量和累加变量一般是同步执行的，累加一次，计数一次.
    三、经典例题导讲
    [例1] 已知三个单元存放了变量，，的值，试给出一个算法，顺次交换，， 的值（即取的值，取的值，取的值），并画出流程图.
    错解：第一步 
      第二步 
    第三步   
    流程图为
                              
                                 图13-1-3
    错因：未理解赋值的含义，由上面的算法使得，均取的值.
    举一形象的例子：有蓝和黑两个墨水瓶，但现在却把蓝墨水装在了黑墨水瓶中，黑墨水错装在了蓝墨水瓶中，要求将其互换，请你设计算法解决这一问题.对于这种非数值性问题的算法设计问题，应当首先建立过程模型，根据过程设计步骤完成算法. 我们不可将两个墨水瓶中的墨水直接交换，因为两个墨水瓶都装有墨水，不可能进行直接交换.正确的解法应为：
    S1 取一只空的墨水瓶，设其为白色；
          S2  将黑墨水瓶中的蓝墨水装入白瓶中；
      S3  将蓝墨水瓶中的黑墨水装入黑瓶中；
      S4  将白瓶中的蓝墨水装入蓝瓶中；
      S5  交换结束.
    正解：第一步       ｛先将的值赋给变量，这时存放的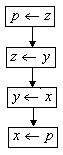单元可作它用} 
       第二步       ｛再将的值赋给，这时存放的单元可作它用} 
    第三步       ｛同样将的值赋给，这时存放的单元可作它用} 
    第四步      ｛最后将的值赋给，三个变量，，的值就完成了交换}
    流程图为
                   
                     图13-1-4
    点评：在计算机中，每个变量都分配了一个存储单元，为了达到交换的目的，需要一个单元存放中间变量.
    [例2]已知三个数，，.试给出寻找这三个数中最大的一个算法，画出该算法的流程图.
     解：流程图为
    
    图13-1-5
    点评：条件结构可含有多个判断框，判断框内的内容要简明、准确、清晰.此题也可将第一个判断框中的两个条件分别用两个判断框表示，两两比较也很清晰.若改为求100个数中的最大数或最小数的问题则选择此法较繁琐，可采用假设第一数最大（最小）将第一个数与后面的数依依比较，若后面的数较大（较小），则进行交换，最终第一个数即为最大（最小）值.
    点评：求和时根据过程的类同性可用循环结构来实现，而不用顺序结构.
    [例3]画出求的值的算法流程图.
    解：这是一个求和问题，可采用循环结构实现设计算法，但要注意奇数项为正号，偶数项为负号.
     思路一：采用-1的奇偶次方（利用循环变量）来解决正负符号问题；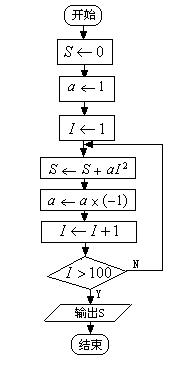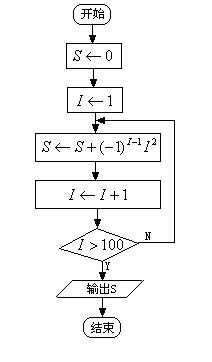
              
          图13-1-6                                      图13-1-7
     思路二：采用选择结构分奇偶项求和；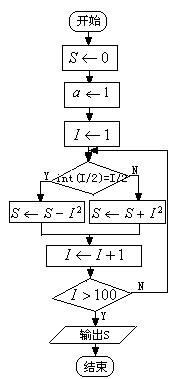
     
          图13-1-8
     思路三：可先将化简成，转化为一个等差数列求和问题，易利用循环结构求出结果.   
    [例4] 设计一算法，求使成立的最小正整数的值.
    解： 流程图为     
    
    图13-1-9
    点评：这道题仍然是考察求和的循环结构的运用问题，需要强调的是求和语句的表示方法.若将题改为求使成立的最大正整数的值时，则需注意的是输出的值.
    [例5]任意给定一个大于1的整数n，试设计一个程序或步骤对n是否为质数做出判断.
    解：算法为：
    S1  判断n是否等于2，若n=2，则n是质数；若n>2，则执行S2
    S2  依次从2～n-1检验是不是的因数，即整除n的数，若有这样的数，则n不是质数；若没有这样的数，则n是质数.
    点评：要验证是否为质数首先必须对质数的本质含义作深入分析：
    （1）质数是只能被1和自身整除的大于1的整数.
    （2）要判断一个大于1的整数n是否为质数，只要根据定义，用比这个整数小的数去除n.如果它只能被1和本身整除，而不能被其它整数整除，则这个数便是质数.
    
               图13-1-10            
    [例6]设计一个求无理数的近似值的算法.
    分析：无理数的近似值可看作是方程的正的近似根，因此该算法的实质是设计一个求方程的近似根的算法.其基本方法即运用二分法求解方程的近似解.
    解：设所求近似根与精确解的差的绝对值不超过0.005,算法:
    S1  令.因为,所以设
    S2  令,判断是否为0,若是,则m为所求;若否,则继续判断大于0还是小于0.
    S3  若>0,则;否则,令.
    S4  判断是否成立，若是，则之间的任意值均为满足条件的近似根；若否，则返回第二步.
    点评：二分法求方程近似解的算法是一个重要的算法案例，将在第三节中详细阐述.
    四、典型习题导练
    1．已知两个单元分别存放了变量和的值，则可以实现变量交换的算法是（   ）.
    A．S1        B．S1         C．S1       D．S1 
      S2           S2             S2          S2
                      S3             S3 
    2.下面流程图中的错误是（  ）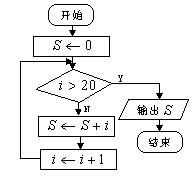
         
    图13-1-11
    A．没有赋值    　B．循环结构有错
    C．S的计算不对    D．判断条件不成立
    3.将“打电话”的过程描述成一个算法，这个算法可表示为                           ，由此说明算法具有下列特性                              .
    4. 在表示求直线（，为常数，且，不同时为0）的斜率的算法
    的流程图中，判断框中应填入的内容是           
    5. 3个正实数，设计一个算法，判断分别以这3个数为三边边长的三角形是否存在，画
    出这个算法的流程图.
    6.一队士兵来到一条有鳄鱼的深河的左岸.只有一条小船和两个小孩，这条船只能承载两个小孩或一个士兵.试设计一个算法，将这队士兵渡到对岸，并将这个算法用流程图表示.
     (责任编辑：admin)



    最近关注
    热点内容