椭圆的参数方程的几点应用
http://www.newdu.com 2025/05/19 06:05:32 人民教育出版社 佚名 参加讨论
椭圆的参数方程的几点应用 贵州省习水县第一中学 袁嗣林 椭圆  的参数方程是 （α是参数， ）。特别地，以点（  ）为圆心，半径是r的椭圆的参数方程是 （α是参数，r>0）。下面就应用做一些归纳。1.参数方程在求最值上的应用 例1 求椭圆  的内接矩形的面积及周长的最大值。分析：此题可以设矩形长为x,然后代入椭圆方程解出宽。但因为有参数a,b,所以把式子列出后都很难解答。而考虑椭圆的参数方程可以迎刃而解。 解：如图，设椭圆 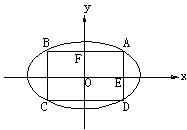 的内接矩形在第一象限的顶点是A（ ）（ ），矩形的面积和周长分别是S、L。  ，当且仅当  时， ， ，此时α存在。点评：利用参数方程后，再利用三角函数性质可以简化求解的过程和降低求解的难度。 例2 设点P（x，y）在椭圆  ，试求点P到直线 的距离d的最大值和最小值。分析：此题可以设点P（x，y）,然后代入椭圆方程 （1），然后利用点到直线的距离公式把d表示出来。但仍然很难继续解答。而考虑椭圆的参数方程却可以树立解决此问题。解：点P（x，y）在椭圆 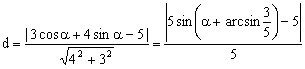上，设点P（ ）（α是参数且 ），则  。当  时，距离d有最小值0，此时椭圆与直线相切；当 时，距离d有最大值2。点评：在求解最值问题时，尤其是求与圆锥曲线有关的函数的最值时，我们可以考虑利用参数方程降低难度。 2.参数方程在求与离心率有关问题上的应用 例3 椭圆 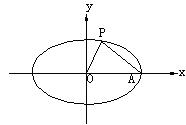与x轴的正向相交于点A，O为坐标原点，若这个椭圆上存在点P，使得OP⊥AP。求该椭圆的离心率e的取值范围。 分析：如果按常规设p(x,y),OP2+AP2=OA2,展开，与离心率没有明显的联系，但用参数方程就非常容易。 解：设椭圆 上的点P的坐标是（）（α≠0且α≠π），A（a，0）。则  。而OP⊥AP，于是  ，整理得 解得  （舍去），或 。因为  ，所以 。可转化为 ，解得 ，于是 。故离心率e的取值范围是 。点评：有关离心率入手比较困难的问题时我们可以考虑应用参数方程求解。 (责任编辑：admin) |
- 上一篇：共线向量的三个命题及应用
- 下一篇：错解剖析得真知（四十）