如何列举基本事件
http://www.newdu.com 2025/05/19 01:05:01 人民教育出版社 佚名 参加讨论
如何列举基本事件 广东省中山一中高中部 许少华 我们知道，求古典概型的概率很重要的一步是列举基本事件，但在具体列举基本事件时，很多同学颇感头痛，特别是面对一些数据较大、涉及的基本事件总数较多时，“列举”可谓举步维艰。稍有疏忽，就给个“小”教训，有没有合适的方法呢？有。这里向你介绍三种常规方法，也许可以让你摆脱困扰。请看： 1.树形图列举法 例1、用1，2，3，4组成的各位数字不重复的四位数，求该四位数中大于3242的概率； 解析：用树形图列举所有满足条件的四位数如下  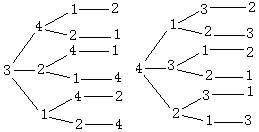 结合树形图，可知所有的四位数分别为：1342，1324，1432，1423，1234，1243，2413，2431，2143，2134，2314，2341，2143，2134，2314，2341，3142，3124，3214，3242，3412，3421， 4132，4123，4312，4321，4231，4213； 由此可得四位数的个数为24个，其中大于3242的有8个，那么，大于3242的概率为  。点评：本题若不借助于树形图，则很难逐一列举。有了树形图，就方便了很多。 类题演练1 从长度分别为3、4、5、7、9的5条线段中任取3条，能构成三角形的概率为（ ） （A）  （B） （C） （D） 解：用树形图列举所有可能的三条线段如下：  结合树形图，可知基本事件为“  ”“ ” “ ” “ ” “ ” “ ”“  ” “ ” “ ” “ ”共10个，其中，有四个“” “” “” “”不能构成三角形；故能构成三角形的概率为 ，选B；2.矩形列举法 例2、从含有三件正品和两件次品的五件产品中，先后任取两件，根据下列条件，求恰有一件正品的概率： （1）第一次抽取是无放回的； （2）第一次抽取是有放回的； 解析：设三件正品分别为A、B、C；两件次品分别为：M、N； （1）第一次抽取是无放回的基本事件如下：  显然，基本事件的总数为  ，其中，同时含A、B、C中一个，再含M、N中一个的基本事件个数为 于是，此时恰有一件正品的概率为  （2）第一次抽取是有放回的基本事件如下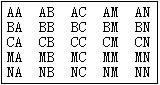：  显然，基本事件的总数为  ，其中，同时含A、B、C中一个，再含M、N中一个的基本事件个数为于是，此时恰有一件正品的概率为  点评：本题的基本事件借助于矩形列举法，通过上述的矩形，很容易揭示基本事件的构成规律，抓住这个规律，很快写出了所有的基本事件。 类题演练2 同时抛两个骰子，求向上的点数之和为  的概率。解：把两个骰子着色红与蓝，用 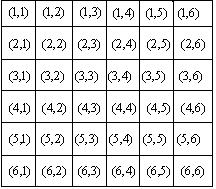 表示红骰子出现的点数，用 表示蓝骰子出现的点数，再用数对 来表示出现的可能结果，其基本事件如下： 共  个结果；将向上的点数之和为的结果记为事件 ；由于，出现向上的点数之和为的结果分别为 、 、 、 、 、 共六种情况；那么  3.三角形列举法 例3、一个盒子里装有标号为1，2，…，9的9个标签，随机的抽取两个 （1）2号签被抽出的概率是多少？ （2）2号签或3号签被抽出的概率是多少？ 解析：基本事件如下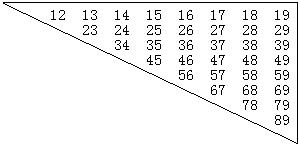：  显然，基本事件的总数为 （1）2号签被抽出的基本事件在三角形中的第二行及第一行中的第一个，共8个。那么，2号签被抽出的概率是  （2）2号签或3号签被抽出的基本事件在三角形中的第二行、第三行及第一行中的前两个，共15个。那么，2号签或3号签被抽出的概率是  点评：本题在列举基本事件中，结合三角形，使基本事件的规律看的非常清楚，因此，写起来也变得轻松、方便。 例4、现从A，B，C，D，E，F六人中选取三人参加一个重要会议，六人被选中的机会相等，求： （1）A 被选中的概率； （2）A和B同时被选中的概率； （3）A或B被选中的概率； 解析：基本事件如下：  显然，基本事件的总数为 （1）“A 被选中” 所包含的基本事件是第一个三角形中的所有事件，其个数为  。那么，A 被选中的概率为 （2）“A和B同时被选中”所包含的基本事件是第一个三角形中第一行的所有事件，其个数为  。那么，A和B同时被选中的概率为 （3）“A或B被选中” 包含的基本事件是第一个三角形与第个三角形中的所有事件，其个数为  。那么，A或B被选中的概率为 点评：本题在列举基本事件中，注意到了三角形列举法的灵活应用。它不是通过一个三角形全部列举的，而是建立在多个三角形的基础上将基本事件全部列出。 类题演练3 一个袋内装有大小相同的6个白球和5个黑球，从中任意抽取2个球，求抽到白球、黑球各一个的概率。 解：用  表示6个白球，用 5个黑球，用三角形列举法，列举的基本事件如下： 显然，基本事件的总数为55；其中白球、黑球各一个的，即既含A又含B的共有30个，因此，抽到白球、黑球各一个的概率为  。(责任编辑：admin) |
- 上一篇：错解剖析得真知（一）
- 下一篇：三角函数定义的应用