浅谈函数单调性的应用
http://www.newdu.com 2025/05/19 11:05:02 人民教育出版社 佚名 参加讨论
浅谈函数单调性的应用 贵州省习水县第一中学 袁嗣林 摘 要：函数的单调性是函数的一条重要性质，本文概括、总结了五种方法判断函数的单调性. 同时对每种方法的特点及适用范围、注意事项采用举例的方式作了具体的介绍，这有助于读者更好地理解和掌握这些方法，从而能轻松的解决有关函数单调性的问题. 关键词：函数单调性；判断方法；应用 On the application of monotone functions Abstract：Monotonicity of the function is an important function of the nature of this sum, summed up the five methods to determine the function of the monotony, while the characteristics of each method and application, note the use made by way of example the specific introduction, which help readers better understand and master these methods, which can easily solve the problem of monotone functions。 Ked Word：Monotonic function; method to judge; application 函数的单调性是函数的一条重要性质，反映了函数值的变化规律. 在高考中历考弥新，考查的深度远远高于课本。 在讨论函数单调性时必须在其定义域内进行，因此要研究函数的单调性就必须先求函数的定义域，函数的单调区间是定义域的子集. 接下来我就来谈谈函数单调性的应用。 一、 函数单调性的判别 单调性是函数最重要的性质之一．导数的引入虽然给单调性的研究带来了极大的方便，但是它并不能解决与单凋性有关的所有问题．本文结合近几年的试题谈谈判断单调性的几种方法。． 1.定义法（自变量增大函数值变小为减函数；反之，为增函数） 例1 判断函数 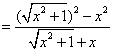 的单调性解 因为  = = ，显然当 为正数且逐渐增加时,   也逐渐增加，则其倒数逐渐减小，即函数值逐渐减小，所以函数 在区间(0，+∞)上为减函数．2.函数变换法 由上面的定义法我们不难得到单调函数运算后的一些结论：在同一个区间上，若f(x)、g(x)都是单凋增(减)函数，则f(x)+g(x)也是单凋增(减)函数；若f(x)单凋递增，g(x)单凋递减，则f(x)-g(x)单调递增；若f(x)单凋递减，g(x)单凋递增，则f(x)-g(x )单调递减. 例2 判断函数  的单调性.解 设  ，显然当x>0时，函数g(x)单凋递增，而函数f(x)单调递减．由上面的运算法则知函数f(X)在区间(0，+∞)上为增函数.3.复合函数法 设函数f(x)由两个函数g(x)与h(X)复合而成，则g(x)与h(x)单调性相同时，f(x)单调递增；g( x)与h(x)单调性不同时，f(x)单调递减，即通常所说的同增异减．多层复合，依此类推． 例3 已知函数y=f(x)的图象与函 数的  图象关于直线 对称，记，若y=g(x)在区间[ 1/2，2]上是增函数，则实数a的取值范围( )(A)（０，+∞） (B)（0，1)U(1，2) (C)  (D) 解 因为  ， 所以  -1  取特殊值     令  则 . 当 ，此时递增，又函数g（t）的图象开口向上，对称轴为 ，所以二次函数g（t）递增，故函数g（x）递增，满足题意.排除A.同理取特殊值 ，排除B，C可知选D.4．作差比较法 根据定义证明函数单调性是判断函数单调性的最重要的方法。其步骤为：(1)设值：即在单调区间上设出两个不相等的自变量  、 ，且< ；(2)比较：即比较 )与 大小，通常采用作差或作商的方法；(3)判断：即根据定义结合前两个步骤得出结论．例4 (由2001年新课程卷题改编) 设  ，求证f(x)在(O，+∞)上是增函数.证明 设0< < ， 则- = + -（ + ）=（ -）+（-）= （ ） 由 > 0，> 0，-> 0， +  0， 10，1- 0所以 -< 0，即)<.从而，f(x)在(0，+∞)上是增函数.5．等价变形法 根据单调性定义，易知增函数的等价形式是  或（-）[ ] 0有时直接用定义判断函数单凋性困难较大，采用等价形式则能帮我们化难为易.例5 设f(x)是定义在[-1，1]上的奇函数，且对任意的a、b∈[-1，1]，当“a+b≠0时，都有  ，试判断单调性.解 设 ，∈[-1，1]，且<，则-∈ [-1，1]，依题意有  = 故  ）在 [-1，1]上是增函数. 二、单调性在解题中的应用 单调性有广泛的应用，主要用于如下几个方面： 1.比较两个数的大小 例6 比较  和 的大小分析 从题设的两个对数，便联想起y=  在 在(O，+∞)上是单调增函数，因此．只要比较两个真数的大小，原题就可获解. 解  ，解得 当 时，有0< < ．因函数y= 在上单调递增，故，.2.证明与正整数有关的命题 例7 已知 ，且 ，  ，n 2 求证 .证明 构造函数  ， 因为x>-1且x≠ 0，故  - = = 所以  ，所以 是单调递减函数.3.解方程 例8 解方程  解  在它们共同的定义域里， 为单调递增函数， 为单调递减函数． 又显然  = ， 所以方程 =仅有一解．X=1．故原方程的解是x=1．4.证明不等式 在证明不等式中，通过联想构造函数，将常量作为变量的瞬时状态，置于构造函数的单调区间内，利用其单调性证明一些不等式，十分便捷． 例9 已知a、b、c∈R ，|a|<1，|b|<1，|c|<1，求证ab+bc+ca+1>0 解 构造函数f(x )=(b+c)x +bc+1，只需证 x∈(-1，1)时f(x)>0恒成立． 当b+c=时， =1一b2 >O恒成立．当b+c≠ 0时，一次函数 = (b+c)x+bc+1，在x∈(-1，1)上是单调的．因为 =bc+b+c+1= (b+1)(c+1)>0，，f(-1)= bc-b-c+1=(b-1)(c-1)>0，所以 =(b+c)x+bc+1在 x∈(-1，1)上恒大于零.综上，当|a|<1时，(b+c)a+bc+1>0恒成立，从而得证． 例10 已知f(x)为R上的减函数,则满足  的实数x的取值范围( )A  B C D 解析 借助单调性将不等式转换为自变量应满足的关系式.很容易可以做出选C. 5.求参数的取值范围 例11 已知f(x)是奇函数，在实数集R上又是单调递减函数，且  时 求t的取值范围.分析： 因已知函数f（x）是奇函数将已知不等式移项后可得    根据 是减函数脱去 ，然后由式子特征构造相应单调函数. 解  < 设x=sin 0<x<1 化简： -3tx<-1 解得 t> .6.已知函数在某区间上单调求参数的取值范围此类问题的本质就是转化为不等式恒成立问题 例12 已知a为实数  若在 和 上都是递增的，求a的取值范围． 解  在和上非负.的图象为开口向上且过点(O，-4)的抛物线，由条件得 即 所以a的取值范围为[-2，2]. 参考文献： ①陈德燕，新专题教程高中数学1/集合与函数（第三版)(全新修订) [M].华东师范大学出版社，2007 ②傅荣强，新课标高中数学函数－龙门专题[M].龙门书局出版社，2008 ③《新阳光专题攻略》编委会，新阳光专题攻略高中数学函数与数列[J].北京教育出版社，2007 ④傅荣强，讲透重点难点高中数学 集合与函数[M].吉林教育出版社，2007 (责任编辑：admin) |
- 上一篇：一道向量问题的解法、引申与拓展
- 下一篇：错解剖析得真知（一）