错解剖析得真知（二十九）_高中学习网-人民教育出版社人教版部编同步解析与测评答案-电子课本资料下载-知识点学习方法与技巧补课解题技巧学习计划表总结-人教网-高中试卷网题库网-中学学科网

错解剖析得真知（二十九）

http://www.newdu.com 2025/05/19 04:05:20 人民教育出版社佚名参加讨论

    错解剖析得真知（二十九）
    §9.3 二项式定理
    一、知识导学
    1.二项式定理：
    上列公式所表示的定理叫做二项式定理.
    右边的多项式叫做的二项展开式，它一共有ｎ＋1项.
    其中各项的系数叫做二项式系数.
    式中的叫做二项展开式的通项，用表示，
    即＝.
    2.二项式系数的性质：
    （1）对称性.与首末两端“等距离”的两个二项式系数相等.事实上，这一性质可直接由公式得到.　
    （2）增减性与最大值. 二项式系数，当ｒ＜时，二项式系数是逐渐增大的.由对称性知它的后半部分是逐渐减小的，且在中间取得最大值.当ｎ是偶数时，中间的一项取得最大值；当ｎ是奇数时，中间的两项相等，且同时取得最大值.
    　（3）各二项式系数的和.
    的展开式的各个二项式系数的和等于.
    二、疑难知识导析
    1．二项式定理是代数公式
    　和

    的概括和推广，它是以乘法公式为基础，以组合知识为工具，用不完全归纳法得到的.同学们可对定理的证明不作要求，但定理的内容必须充分理解.
    2．对二项式定理的理解和掌握，要从项数、系数、指数、通项等方面的特征去熟悉它的展开式.通项公式＝在解题时应用较多，因而显得尤其重要，但必须注意，它是的二项展开式的第ｒ＋1项，而不是第ｒ项.
    3．二项式定理的特殊表示形式
    （1）.
    这时通项是＝.
    （2）.
    这时通项是＝.
    （3）.
    即各二项式系数的和为.
    4．二项式奇数项系数的和等于二项式偶数项系数的和.即

    三、经典例题导讲
    [例1]已知，
    求的值.
    错解：由二项展开式的系数的性质可知：的展开式的各个二项式系数的和等于，显然，就是展开式中的，因此的值为－1.
    错因：上述解答忽略了是项的系数，而不是二项式系数.
    正解：由二项展开式的结构特征，是项的系数，而不是二项式系数.观察式子特征，如果＝1，则等式右边为，出现所求式子的形式，而就是展开式中的，因此，即
    1＝1＋，所以，＝0
    评注　这是二项式定理的一个典型应用—赋值法，在使用赋值法时，令、ｂ等于多少，应就具体问题而定，有时取“1”，有时取“－1”，或其他值.
    [例2]在多项式的展开式中，含项的系数为　　　　.
    错解：原式＝＝　　
    ∴项的系数为0.
    错因：忽视了ｎ的范围，上述解法得出的结果是在ｎ不等于6的前提下得到的，而这个条件并没有提供.
    正解：原式＝＝　　
    ∴当ｎ≠6时，项的系数为0.
    当ｎ＝6时，项的系数为1
    说明：本解法体现了逆向运用二项式定理的灵活性，应注意原式中对照二项式定理缺少这一项.
    [例3] 的末尾连续零的个数是    (      )
    A．7          B．5          C．3             D．2
    解：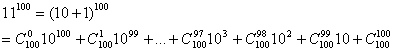
    上述展开式中，最后一项为1；倒数第二项为1000；倒数第三项为495000，末尾有三个0；倒数第四项为16170000，末尾有四个0；依次前面各项末尾至少有四个0.所以的末尾连续零的个数是3.　　　故选C.
    [例4] 已知的展开式前三项中的的系数成等差数列.
    （1）求展开式中所有的的有理项；
    （2）求展开式中系数最大的项.
    解：（1）展开式前三项的系数分别为
    .
    由题设可知：
    解得：ｎ＝8或ｎ＝1（舍去）.
    当ｎ＝8时，＝.
    据题意，4－必为整数，从而可知必为4的倍数，
    而0≤≤8，∴＝0,4，8.
    故的有理项为：，，.
    （2）设第＋1项的系数最大，显然＞0，
    故有≥1且≤1.
    ∵＝，
    由≥1，得≤3.
    ∵＝，
    由≤1，得≥2.
    ∴＝2或＝3，所求项分别为和.
    评注：1.把握住二项展开式的通项公式，是掌握二项式定理的关键，除通项公式外，还应熟练掌握二项式的指数、项数、展开式的系数间的关系、性质.
    2.运用通项公式求二项展开的特定项，如求某一项，含某次幂的项，常数项，有理项，系数最大的项等，一般是运用通项公式根据题意列方程，在求得ｎ或ｒ后，再求所需的项（要注意ｎ和ｒ的数值范围及大小关系）.
    3.注意区分展开式“第＋1项的二项式系数”与“第＋1项的系数”.
    [例5]已知的展开式中含项的系数为24，求展开式中含项的系数的最小值.
    解：解法一　由中含项的系数为24，可得
    .从而，.
    设中含项的系数为ｔ，则
    ｔ＝.
    把代入上式，得
    ｔ＝.
    ∴当ｎ＝6时，ｔ的最小值为120，此时ｍ＝ｎ＝6.
    解法二　由已知，
    设中含项的系数为ｔ，则
    ｔ＝≥2＝2（72－12）＝120.
    当且仅当ｍ＝ｎ＝6时，ｔ有最小值120.
    ∴展开式中含项的系数的最小值为120.
    评注：构造函数法是一种常用的方法，尤其在求最值问题中应用非常广泛.
    四、典型习题导练
    1．化简：
    2. 设，则
    的值为
    3. （1+x）(2+x)(3+x)…(20+x)的展开式中x¹⁹的系数是                        .
    4. 式子的展开式中的常数项是　　　（　　　）
    A、－15　　　B、20　　　C、－20　　　　D、15
    5．已知二项式中，＞0，ｂ＞0,2ｍ＋ｎ＝0但ｍｎ≠0，若展开式中的最大系数项是常数项，求的取值范围.
    6．用二项式定理证明：能被整除　　（ｎ∈，ｎ≥2）.　
     (责任编辑：admin)

错解剖析得真知（二十九）

http://www.newdu.com 2025/05/19 04:05:20 人民教育出版社 佚名 参加讨论

http://www.newdu.com 2025/05/19 04:05:20 人民教育出版社佚名参加讨论