三角函数诱导公式揭秘
http://www.newdu.com 2025/05/19 11:05:24 人民教育出版社 佚名 参加讨论
三角函数诱导公式揭秘 熊明军 无论在哪本教材中，三角函数诱导公式这一节所涉及到的公式都是相当得多。在许多参考书里共同提到了记忆诱导公式的统一口诀：“奇变偶不变，符号看象限”。多少年来，参考书这么写，老师们这么教，但是教材却从没有简化，原因何在？ 本文首先对该口诀进行必要的介绍，然后尝试去探寻众多诱导公式的联系及内涵，进而对教材内容的编排提出自己的理解。 一、口诀解析 任意一个角都可以表示为  的形式。当把任意角化为该形式后，利用口诀“奇变偶不变，符号看象限”，就能把任意角转化到 之间，即初中所学，学生熟悉的锐角三角函数值问题了。下面对该口诀进行必要的解析： ①“奇”与“偶”：是指把任意角化为 的形式中 的奇偶性，即是奇数还是偶数；②“变”与“不变”：是指三角函数的名称改变与否，即若变，则正弦变余弦、余弦变正弦、正切变余切、余切变正切。 综合①②，“奇变偶不变”是说，把任意角化为  的形式后，若是奇数则三角函数名称改变，若是偶数则三角函数名称不改变。③“象限”：是指把任意角化为 的形式后，假设 时，所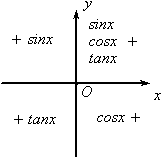在的象限。④“符号”：是指在确定 所在的象限后，相应的原三角函数值的符号（如下图）。 二、诱导公式的内在联系 教材中所给的诱导公式，集中体现了数学中的化归与转化思想。在求任意角的三角函数值时，其基本思路为：负角  正角 内的角内的角。根据这个思路，运用口诀“奇变偶不变，符号看象限”化简，就不可能充分地体现出来，并且在口诀中，任意角所在象限的判断也是相当麻烦的。 下面，针对教材中所给的三角函数诱导公式及化归与转化思路，将它们划分为三类诱导公式。 ①名不变，奇  偶 （繁角简角）如果任意角可以表示成  ，即含有 的整数倍，则选用第一类诱导公式。利用该公式可将繁杂角化为简单的角。第一类诱导公式：正弦函数、余弦函数的名称不改变，化简后的符号随 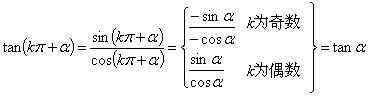的奇偶性而改变──奇数、偶数。即 ， ；可得：  .②名改变，正 余（钝角锐角）利用其余诱导公式先化简，若出现  的形式，即含有 ，则选用第二类诱导公式。该公式是开篇口诀的特例。第二类诱导公式：正弦函数、余弦函数的名称改变，化简后的符号由原式三角函数名确定──正弦 、余弦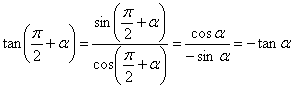。即 ；可得：  .③奇偶性，正奇余偶（负角 正角）对于函数  ，若函数为奇函数，则 ；若函数为偶函数，则 。第三类诱导公式：正弦函数为奇函数；余弦函数为偶函数。即  ；可得：  .综上所述，三角函数诱导公式只需要三类即可将负角 正角 内的角 内的角。即第一类： ，；第二类： ；第三类： .三、三类诱导公式的简单运用 诱导公式一：  解析 将正切化为弦，即  。利用第一类诱导公式，名不变，因为的系数 是偶数，为正，所以  .诱导公式二：  解析 第一类诱导公式，名不变，因为 的系数 是奇数，为负，所以 诱导公式四：  解析 将减法变为加法，即  。利用第一类诱导公式，名不变，因为的系数是奇数，为负，所以 ；利用第三类诱导公式，因为余弦函数为偶函数，所以 .诱导公式五：  解析 将减法变为加法，即  。利用第二类诱导公式，名改变，正弦，所以 ；利用第三类诱导公式，因为余弦函数是偶函数，所以 .例：化简  。解析  ，首先利用第一类诱导公式,名不变，又因为的系数 是奇数，符号为负，所以 ；然后利用第二类诱导公式，名改变，余弦，所以 .注意：在应用三类诱导公式时，必须抓住①第一类诱导公式：任意角能分离出 的整数倍；②第二类诱导公式：任意角能分离出；③与也是选择诱导公式的依据。(责任编辑：admin) |
- 上一篇：错解剖析得真知（三十）
- 下一篇：一个最优化问题的解法探讨