错解剖析得真知(三十一)
第十章 导数及其应用
§10.1导数及其运算
一、知识导学
1.瞬时变化率:设函数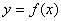 在 在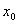 附近有定义,当自变量在 附近有定义,当自变量在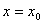 附近改变量为 附近改变量为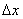 时,函数值相应地改变 时,函数值相应地改变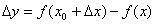 ,如果当 ,如果当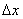 趋近于0时,平均变化率 趋近于0时,平均变化率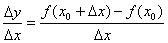 趋近于一个常数c(也就是说平均变化率与某个常数c的差的绝对值越来越小,可以小于任意小的正数),那么常数c称为函数 趋近于一个常数c(也就是说平均变化率与某个常数c的差的绝对值越来越小,可以小于任意小的正数),那么常数c称为函数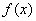 在点 在点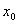 的瞬时变化率。 的瞬时变化率。
2.导数:当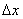 趋近于零时, 趋近于零时,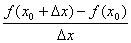 趋近于常数c。可用符号“ 趋近于常数c。可用符号“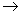 ”记作:当 ”记作:当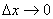 时, 时,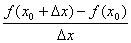 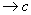 或记作 或记作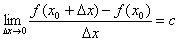 ,符号“ ,符号“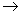 ”读作“趋近于”。函数在 ”读作“趋近于”。函数在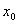 的瞬时变化率,通常称作 的瞬时变化率,通常称作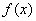 在 在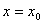 处的导数,并记作 处的导数,并记作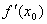 。 。
3.导函数:如果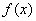 在开区间 在开区间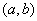 内每一点 内每一点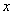 都是可导的,则称 都是可导的,则称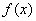 在区间 在区间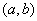 可导。这样,对开区间 可导。这样,对开区间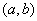 内每个值 内每个值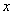 ,都对应一个确定的导数 ,都对应一个确定的导数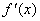 。于是,在区间 。于是,在区间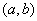 内, 内,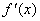 构成一个新的函数,我们把这个函数称为函数 构成一个新的函数,我们把这个函数称为函数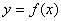 的导函数。记为 的导函数。记为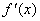 或 或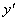 (或 (或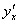 )。 )。
4.导数的四则运算法则:1)函数和(或差)的求导法则:设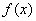 , ,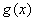 是可导的,则 是可导的,则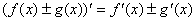 即,两个函数的和(或差)的导数,等于这两个函数的导数的和(或差)。 即,两个函数的和(或差)的导数,等于这两个函数的导数的和(或差)。
2)函数积的求导法则:设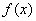 , ,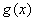 是可导的,则 是可导的,则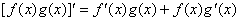 即,两个函数的积的导数,等于第一个函数的导数乘上第二个函数,加上第一个函数乘第二个函数的导数。 即,两个函数的积的导数,等于第一个函数的导数乘上第二个函数,加上第一个函数乘第二个函数的导数。
3)函数的商的求导法则:设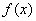 , ,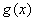 是可导的, 是可导的, ,则 ,则
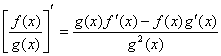
5.复合函数的导数:设函数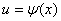 在点 在点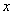 处有导数 处有导数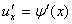 ,函数 ,函数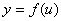 在点 在点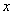 的对应点 的对应点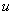 处有导数 处有导数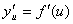 ,则复合函数 ,则复合函数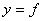 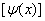 在点 在点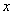 处有导数,且 处有导数,且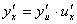 . .
6.几种常见函数的导数:
(1) (2) (2)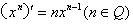
(3)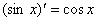 (4) (4)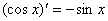
(5)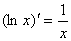 (6) (6)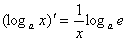
(7)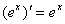 (8) (8)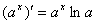
二、疑难知识导析
1.导数的实质是函数值相对于自变量的变化率
2.运用复合函数的求导法则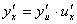 ,应注意以下几点 ,应注意以下几点
(1)利用复合函数求导法则求导后,要把中间变量换成自变量的函数,层层求导.
(2) 要分清每一步的求导是哪个变量对哪个变量求导,不能混淆,一直计算到最后,常出现如下错误,如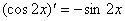 实际上应是 实际上应是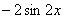 。 。
(3) 求复合函数的导数,关键在于分清楚函数的复合关系,选好中间变量,如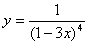 选成 选成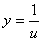 , ,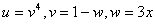 计算起来就复杂了。 计算起来就复杂了。
3.导数的几何意义与物理意义
导数的几何意义,通常指曲线的切线斜率.导数的物理意义,通常是指物体运动的瞬时速度。对导数的几何意义与物理意义的理解,有助于对抽象的导数定义的认识,应给予足够的重视。
4.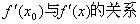
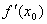 表示 表示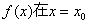 处的导数,即 处的导数,即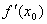 是函数在某一点的导数; 是函数在某一点的导数;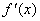 表示函数 表示函数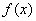 在某给定区间 在某给定区间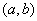 内的导函数,此时 内的导函数,此时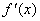 是在 是在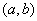 上 上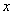 的函数,即 的函数,即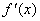 是在 是在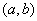 内任一点的导数。 内任一点的导数。
5.导数与连续的关系
若函数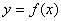 在 在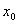 处可导,则此函数在点 处可导,则此函数在点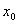 处连续,但逆命题不成立,即函数 处连续,但逆命题不成立,即函数
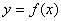 在点 在点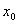 处连续,未必在 处连续,未必在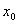 点可导,也就是说,连续性是函数具有可导性的必要条件,而不是充分条件。 点可导,也就是说,连续性是函数具有可导性的必要条件,而不是充分条件。
6.可以利用导数求曲线的切线方程
由于函数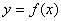 在 在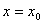 处的导数,表示曲线在点 处的导数,表示曲线在点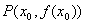 处切线的斜率,因 处切线的斜率,因
此,曲线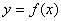 在点 在点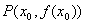 处的切线方程可如下求得: 处的切线方程可如下求得:
(1)求出函数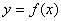 在点 在点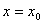 处的导数,即曲线 处的导数,即曲线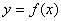 在点 在点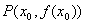 处切线的斜率。 处切线的斜率。
(2)在已知切点坐标和切线斜率的条件下,求得切线方程为: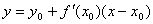 ,如果曲线 ,如果曲线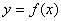 在点 在点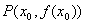 的切线平行于 的切线平行于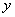 轴(此时导数不存在)时,由切线定义可知,切线方程为 轴(此时导数不存在)时,由切线定义可知,切线方程为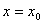 . .
三、经典例题导讲
[例1]已知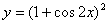 ,则 ,则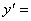 . .
错因:复合函数求导数计算不熟练,其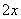 与 与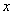 系数不一样也是一个复合的过程,有的同学忽视了,导致错解为: 系数不一样也是一个复合的过程,有的同学忽视了,导致错解为: . .
正解:设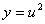 , ,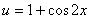 ,则 ,则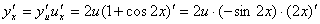
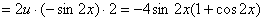  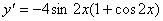 . .
[例2]已知函数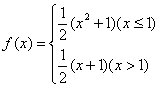 判断f(x)在x=1处是否可导? 判断f(x)在x=1处是否可导?
错解: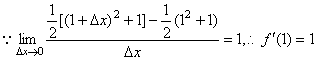 。 。
分析: 分段函数在“分界点”处的导数,须根据定义来判断是否可导 .
解: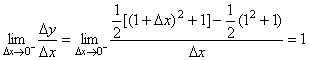
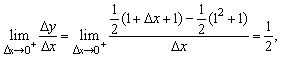
∴ f(x)在x=1处不可导.
注: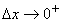 ,指 ,指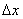 逐渐减小趋近于0; 逐渐减小趋近于0;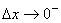 ,指 ,指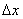 逐渐增大趋近于0。 逐渐增大趋近于0。
点评:函数在某一点的导数,是一个极限值,即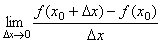 ,△x→0,包括△x→0+,与△x→0-,因此,在判定分段函数在“分界点”处的导数是否存在时,要验证其左、右极限是否存在且相等,如果都存在且相等,才能判定这点存在导数,否则不存在导数. ,△x→0,包括△x→0+,与△x→0-,因此,在判定分段函数在“分界点”处的导数是否存在时,要验证其左、右极限是否存在且相等,如果都存在且相等,才能判定这点存在导数,否则不存在导数.
[例3]求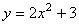 在点 在点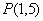 和 和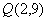 处的切线方程。 处的切线方程。
错因:直接将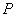 , ,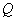 看作曲线上的点用导数求解。 看作曲线上的点用导数求解。
分析:点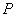 在函数的曲线上,因此过点 在函数的曲线上,因此过点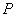 的切线的斜率就是 的切线的斜率就是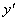 在 在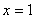 处的函数值; 处的函数值;
点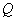 不在函数曲线上,因此不能够直接用导数求值,要通过设切点的方法求切线. 不在函数曲线上,因此不能够直接用导数求值,要通过设切点的方法求切线.
解: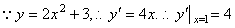
即过点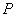 的切线的斜率为4,故切线为: 的切线的斜率为4,故切线为: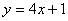 . .
设过点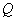 的切线的切点为 的切线的切点为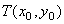 ,则切线的斜率为 ,则切线的斜率为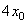 ,又 ,又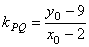 , ,
故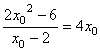 , ,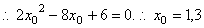 。 。
即切线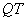 的斜率为4或12,从而过点 的斜率为4或12,从而过点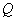 的切线为: 的切线为:
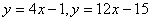
点评: 要注意所给的点是否是切点.若是,可以直接采用求导数的方法求;不是则需设出切点坐标.
[例4]求证:函数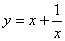 图象上的各点处切线的斜率小于1,并求出其斜率为0的切线方程. 图象上的各点处切线的斜率小于1,并求出其斜率为0的切线方程.
分析: 由导数的几何意义知,要证函数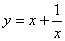 的图象上各点处切线的斜率都小于1,只要证它的导函数的函数值都小于1,因此,应先对函数求导后,再进行论证与求解. 的图象上各点处切线的斜率都小于1,只要证它的导函数的函数值都小于1,因此,应先对函数求导后,再进行论证与求解.
解:(1)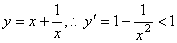 ,即对函数 ,即对函数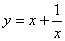 定义域内的任一 定义域内的任一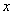 ,其导数值都小于 ,其导数值都小于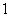 ,于是由导数的几何意义可知,函数 ,于是由导数的几何意义可知,函数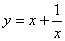 图象上各点处切线的斜率都小于1. 图象上各点处切线的斜率都小于1.
(2)令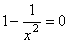 ,得 ,得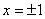 ,当 ,当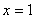 时, 时,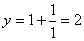 ;当 ;当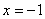 时, 时,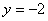 , ,
 曲线 曲线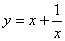 的斜率为0的切线有两条,其切点分别为 的斜率为0的切线有两条,其切点分别为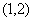 与 与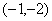 ,切线方程分别为 ,切线方程分别为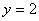 或 或 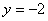 。 。
点评: 在已知曲线 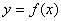 切线斜率为 切线斜率为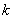 的情况下,要求其切线方程,需要求出切点,而切点的横坐标就是 的情况下,要求其切线方程,需要求出切点,而切点的横坐标就是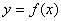 的导数值为 的导数值为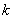 时的解,即方程 时的解,即方程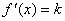 的解,将方程 的解,将方程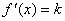 的解代入 的解代入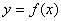 就可得切点的纵坐标,求出了切点坐标即可写出切线方程,要注意的是方程 就可得切点的纵坐标,求出了切点坐标即可写出切线方程,要注意的是方程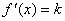 有多少个相异实根,则所求的切线就有多少条. 有多少个相异实根,则所求的切线就有多少条.
[例5](02年高考试题)已知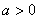 ,函数 ,函数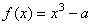 , ,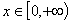 ,设 ,设 ,记曲线 ,记曲线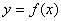 在点 在点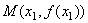 处的切线为 处的切线为 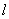 . .
(1)求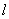 的方程; 的方程;
(2)设 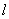 与 与 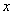 轴交点为 轴交点为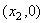 ,求证: ,求证:
① 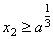 ; ②若 ; ②若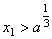 ,则 ,则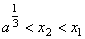
分析:本题考查导数的几何意义,利用其求出切线斜率,导出切线方程 .
解:(1)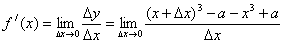
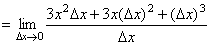
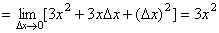
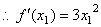  切线 切线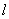 的方程为 的方程为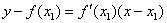
即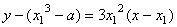 . .
(2)①依题意,切线方程中令y=0得,
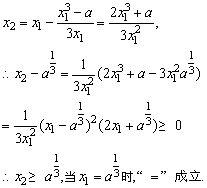
②由①知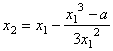 , ,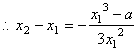
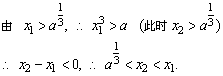
[例6]求抛物线 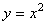 上的点到直线 上的点到直线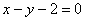 的最短距离. 的最短距离.
分析:可设 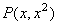 为抛物线上任意一点,则可把点 为抛物线上任意一点,则可把点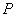 到直线的距离表示为自变量 到直线的距离表示为自变量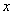 的函数,然后求函数最小值即可,另外,也可把直线向靠近抛物线方向平移,当直线与抛物线相切时的切点到直线 的函数,然后求函数最小值即可,另外,也可把直线向靠近抛物线方向平移,当直线与抛物线相切时的切点到直线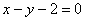 的距离即为本题所求. 的距离即为本题所求.
解:根据题意可知,与直线 x-y-2=0平行的抛物线y=x2的切线对应的切点到直线x-y-2=0的距离最短,设切点坐标为(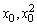 ),那么 ),那么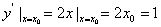 ,∴ ,∴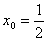
∴ 切点坐标为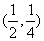 ,切点到直线x-y-2=0的距离 ,切点到直线x-y-2=0的距离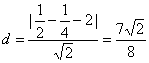 , ,
∴ 抛物线上的点到直线的最短距离为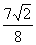 . .
四、典型习题导练
1.函数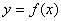 在 在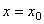 处不可导,则过点 处不可导,则过点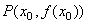 处,曲线 处,曲线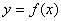 的切线 ( ) 的切线 ( )
A.必不存在 B.必定存在 C.必与x轴垂直 D.不同于上面结论
2.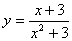 在点x=3处的导数是____________. 在点x=3处的导数是____________.
3.已知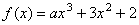 ,若 ,若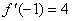 ,则 ,则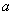 的值为____________. 的值为____________.
4.已知P(-1,1),Q(2,4)是曲线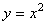 上的两点,则与直线 上的两点,则与直线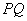 平行的曲线 平行的曲线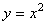 的切线方程是 _____________. 的切线方程是 _____________.
5.如果曲线 的某一切线与直线 的某一切线与直线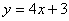 平行,求切点坐标与切线方程. 平行,求切点坐标与切线方程.
6.若过两抛物线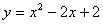 和 和 的一个交点为P的两条切线互相垂直.求证:抛物线 的一个交点为P的两条切线互相垂直.求证:抛物线 过定点 过定点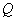 ,并求出定点 ,并求出定点 的坐标. 的坐标.
(责任编辑:admin)
|
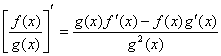
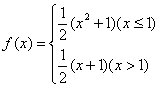 判断f(x)在x=1处是否可导?
判断f(x)在x=1处是否可导?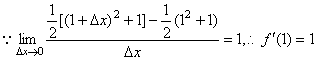 。
。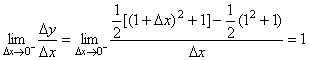
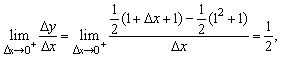
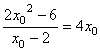 ,
,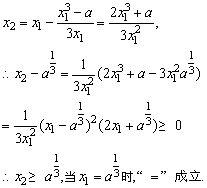
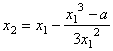 ,
,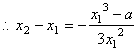
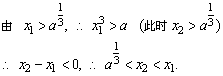
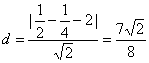 ,
,