错解剖析得真知(三十二)
http://www.newdu.com 2025/05/19 11:05:28 人民教育出版社 佚名 参加讨论
错解剖析得真知(三十二) §10.2导数的应用 一、 知识导学 1.可导函数的极值 (1)极值的概念 设函数 (2)求可导函数 ①求导数 ②求方程 ③检验 2.函数的最大值和最小值 (1)设 ①求 ②将 (2)若函数 二、疑难知识导析 1.在求可导函数的极值时,应注意:(以下将导函数 (1) 可导函数的驻点可能是它的极值点,也可能不是极值点。例如函数 (2) 求一个可导函数的极值时,常常把驻点附近的函数值的讨论情况列成表格,这样可使函数在各单调区间的增减情况一目了然. (3) 在求实际问题中的最大值和最小值时,一般是先找出自变量、因变量,建立函数关系式,并确定其定义域.如果定义域是一个开区间,函数在定义域内可导(其实只要是初等函数,它在自己的定义域内必然可导),并且按常理分析,此函数在这一开区间内应该有最大(小)值(如果定义域是闭区间,那么只要函数在此闭区间上连续,它就一定有最大(小).记住这个定理很有好处),然后通过对函数求导,发现定义域内只有一个驻点,那么立即可以断定在这个驻点处的函数值就是最大(小)值。知道这一点是非常重要的,因为它在应用上较为简便,省去了讨论驻点是否为极值点,求函数在端点处的值,以及同函数在极值点处的值进行比较等步骤. 2.极大(小)值与最大(小)值的区别与联系 极值是局部性概念,最大(小)值可以看作整体性概念,因而在一般情况下,两者是有区别的.极大(小)值不一定是最大(小)值,最大(小)值也不一定是极大(小)值,但如果连续函数在区间 三、经典例题导讲 [例1]已知曲线 错解: 错因:曲线在某点处的切线斜率是该曲线对应的函数在该点处的导数值,这是导数的几何意义.在此题中,点 正解:设过点 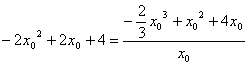 化简,得 [例2]已知函数 错解: 正解: [例3]当 证明: 点评:由题意构造出两个函数 [例4]设工厂到铁路线的垂直距离为20km,垂足为B.铁路线上距离B为100km处有一原料供应站C,现要在铁路BC之间某处D修建一个原料中转车站,再由车站D向工厂修一条公路.如果已知每千米的铁路运费与公路运费之比为3:5,那么,D应选在何处,才能使原料供应站C运货到工厂A所需运费最省? 解 : 设BD之间的距离为 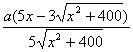 ,令 ,令点评: 这是一道实际生活中的优化问题,建立的目标函数是一个复合函数,用过去的知识求其最值往往没有一般方法,即使能求出,也要涉及到较高的技能技巧.而运用导数知识,求复合函数的最值就变得非常简单.一般情况下,对于实际生活中的优化问题,如果其目标函数为高次多项式函数、简单的分式函数简单的无理函数、简单的指数、对数函数,或它们的复合函数,均可用导数法求其最值.由此也可见,导数的引入,大大拓宽了中学数学知识在实际优化问题中的应用空间. [例5](2006年四川)函数 (2)设 解:(1)由题意 令 对 ∴ 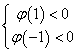 即 即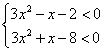 解得 故 (2) ①当 ②当
∴ 又∵ ∴当 当 由题意得 即 解得 综上, [例6]若电灯B可在桌面上一点O的垂线上移动,桌面上有与点O距离为 分析:如图,由光学知识,照度 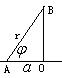 解:设 于是 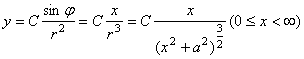 , ,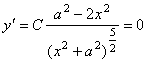 . .当
点评:在有关极值应用的问题中,绝大多数在所讨论的区间上函数只有一点使得 四、典型习题导练 1.已知函数 A.2 B.-2 C. 2.已知函数 3.给出下列三对函数:① ③ 4.已知函数 5.已知抛物线 6.设 (1)求 §10.3定积分与微积分基本定理 一、知识导学 1.可微:若函数 2.微积分基本定理:如果 由于 二、疑难知识导析 1 .定积分的定义过程包括“分割、近似求和、取极限”这几个步骤,这里包含着很重要的数学思想方法,只有对定积分的定义过程了解了,才能掌握定积分的应用. 1)一般情况下,对于区间的分割是任意的,只要求分割的小区间的长度的最大者 2)对每个小区间内 3)求极限的时候,不是 2.在微积分基本定理中,原函数不是唯一的,但我们只要选取其中的一个就可以了,一般情况下选那个不带常数的。因为 3.利用定积分来求面积时,特别是位于 三 、经典例题导讲 [例1]求曲线 错解:分两部分,在 分析:面积应为各部分积分的代数和,也就是第二部分的积分不是阴影部分的面积,而是面积的相反数。所以不应该将两部分直接相加。 正解: [例2]用微积分基本定理证明 分析:即寻找 解;设 = 由微积分基本定理的逆运用可知:上式 所以原式成立,即证。 注:该式可用来求分布在 [例3]根据等式求常数 1) 分析:利用微积分基本定理,求出原函数代入 解:1) 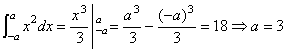 2) [例4]某产品生产x个单位时的边际收入 (1) 求生产了50个单位时的总收入。 (2) 如果已生产了100个单位时,求再生产100个单位时的总收入。 分析:总收入为边际收入的积分和,求总收入既为求边际收入在规定时间内的定积分。由收入函数 (1)生产50个单位时的总收入为 = (2)已生产了100个单位时后,再生产100个单位时的总收入为 答:生产50个单位时的总收入为99875;生产了100个单位时后,再生产100个单位时的总收入为19850. |
- 上一篇:巧构奇函数简解一类问题
- 下一篇:三角形垂心的性质总结