由圆类比出有心曲线的几个性质
湖北省阳新县高级中学 邹生书
波利亚说:“类比是一个伟大的引路人”, “类比是获得发现的伟大源泉”.类比在科学创造的发明与发现中有着十分广泛的应用.毫不例外,在数学领域中也有着广泛的应用.数学中应用类比方法的关键,是要善于发现两个不同数学对象在空间形式或数量关系之间的“相似”, 而这种“相似”并不是简单的模仿和复制,而是富有创造性的设想和探究.
在有心圆锥曲线中,圆是最简单的图形,本文笔者借助类比从圆中我们熟悉的几个性质出发,类比出椭圆、双曲线的几个类似性质.
1.我们知道:若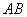 是 是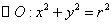 的任意一条直径,点 的任意一条直径,点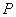 是圆上任意一点, 则 是圆上任意一点, 则 ,若直线 ,若直线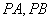 的斜率都存在,则 的斜率都存在,则 . .
怎样将此性质类比到椭圆上呢?若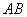 是椭圆 是椭圆 的任意一条直径,点 的任意一条直径,点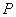 是椭圆上任意一点,显然 是椭圆上任意一点,显然 ;若直线 ;若直线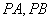 的斜率都存在,显然 的斜率都存在,显然 ,那么 ,那么 是否为定值呢? 是否为定值呢?
设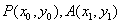 ,因为 ,因为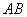 是椭圆的直径,所以点 是椭圆的直径,所以点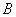 的坐标为 的坐标为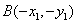 ,所以 ,所以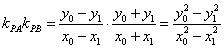 .又因为点 .又因为点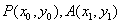 在椭圆上,所以有 在椭圆上,所以有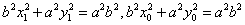 ,两式相减得, ,两式相减得, ,所以 ,所以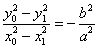 ,所以 ,所以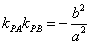 .于是有如下结论: .于是有如下结论:
性质1.1 已知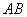 是椭圆 是椭圆 的直径,点 的直径,点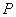 是椭圆上任意一点,若直线 是椭圆上任意一点,若直线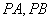 的斜率都存在,则 的斜率都存在,则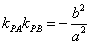 . .
同理可证双曲线也有如下类似性质:
性质1.2 已知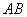 是双曲线 是双曲线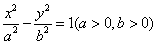 的直径,点 的直径,点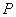 是双曲线上任意一点,若直线 是双曲线上任意一点,若直线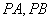 的斜率都存在,则 的斜率都存在,则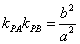 . .
2.我们知道:若直线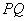 与 与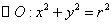 相切于点 相切于点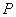 ,则有 ,则有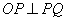 ,若直线 ,若直线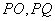 的斜率都存在,则 的斜率都存在,则 . .
如何将此性质成功类比到椭圆呢?若直线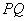 与椭圆 与椭圆 相切于点 相切于点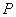 ,显然 ,显然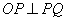 不成立;若直线 不成立;若直线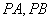 的斜率都存在,显然 的斜率都存在,显然 .那么 .那么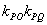 是否为定值呢? 是否为定值呢?
设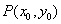 ,则切线 ,则切线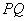 的方程为: 的方程为: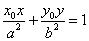 ,所以 ,所以 ,又 ,又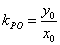 ,所以 ,所以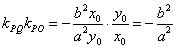 ,于是有如下结论: ,于是有如下结论:
性质2.1 若直线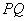 与椭圆 与椭圆 相切于点 相切于点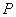 ,且直线 ,且直线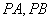 的斜率都存在,则有 的斜率都存在,则有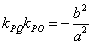 . .
同理可证双曲线也有如下类似性质:
性质2.2 若直线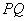 与双曲线 与双曲线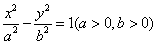 相切于点 相切于点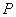 ,且直线 ,且直线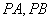 的斜率都存在,则有 的斜率都存在,则有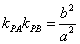 . .
3.我们又知道:若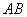 是 是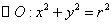 的非直径的弦,点 的非直径的弦,点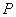 是弦 是弦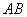 的中点,则有则有 的中点,则有则有 ,若直线 ,若直线 的斜率都存在,则 的斜率都存在,则 . .
将此性质类比到椭圆、双曲线有如下性质:
性质3.1 若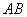 是椭圆 是椭圆 上的非直径的弦,点 上的非直径的弦,点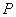 是弦 是弦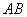 的中点,且直线 的中点,且直线 的斜率都存在,则 的斜率都存在,则 . .
证明 设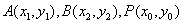 ,则有 ,则有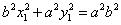 ①, ①, ②, ②,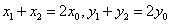 ,将①式减②式得, ,将①式减②式得,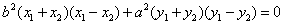 ,所以 ,所以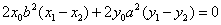 所以 所以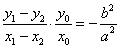 ,即 ,即 . .
性质3.2 若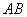 是双曲线 是双曲线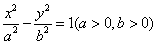 上的非直径的弦,点 上的非直径的弦,点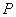 是弦 是弦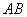 的中点,若直线 的中点,若直线 的斜率都存在,则 的斜率都存在,则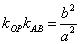 . .
4.我们还知道:已知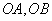 是 是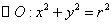 的两条半径,圆在 的两条半径,圆在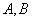 两点处的切线相交于点 两点处的切线相交于点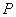 ,(1)若 ,(1)若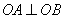 ,则 ,则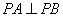 ,若直线 ,若直线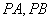 的斜率都存在,则 的斜率都存在,则 ; ;
(2)若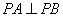 ,则 ,则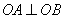 . .
将此性质类比到椭圆、双曲线可得如下性质:
性质4.1 已知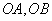 是椭圆 是椭圆 的两条半径,椭圆在 的两条半径,椭圆在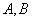 两点处的切线相交于点 两点处的切线相交于点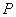 ,且直线 ,且直线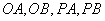 的斜率都存在,则 的斜率都存在,则 . .
证明 因为直线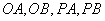 的斜率都存在,设 的斜率都存在,设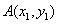 ,则椭圆在点 ,则椭圆在点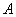 处的切线方程为 处的切线方程为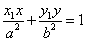 ,所以 ,所以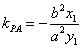 ,设 ,设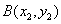 ,同理可得椭圆在点 ,同理可得椭圆在点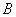 处的切线斜率为 处的切线斜率为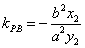 ,所以 ,所以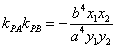 .因为 .因为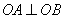 所以 所以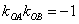 ,即 ,即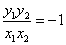 ,从而 ,从而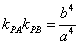 . .
性质4.2 若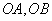 是双曲线 是双曲线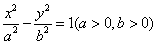 的两条半径,双曲线在 的两条半径,双曲线在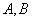 两点处的切线相交于点 两点处的切线相交于点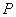 .(1)若 .(1)若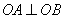 ,且直线 ,且直线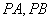 的斜率都存在,则 的斜率都存在,则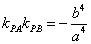 ;(2)若 ;(2)若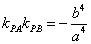 ,则 ,则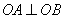 . .
下面我们以2010年高考题为例来说明本文类比得到的性质在解题中的应用.
例1 (2010年高考宁夏卷理科第12题)已知双曲线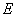 的中心为原点, 的中心为原点,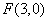 是 是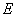 的焦点,过 的焦点,过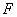 的直线 的直线 与 与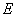 相交于 相交于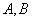 两点,且 两点,且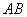 的中点为 的中点为 ,则 ,则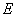 的方程为( ) 的方程为( )
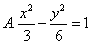 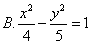 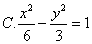 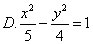
解 设曲线方程为 , ,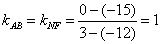 , ,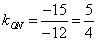 ,由本文性质3.2有 ,由本文性质3.2有 ,所以 ,所以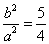 ,又因为 ,又因为 ,所以 ,所以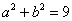 ,联立解得 ,联立解得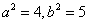 ,故所求曲线 ,故所求曲线 的方程为 的方程为 ,故应选 ,故应选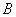 . .
例2(2010年安徽高考理科第19题)已知椭圆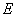 经过点 经过点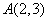 ,对称轴为坐标轴,焦点 ,对称轴为坐标轴,焦点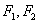 在 在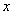 轴上,离心率 轴上,离心率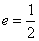 . .
(Ⅰ)求椭圆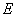 的方程; 的方程;
(Ⅱ)求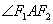 角平分线所在直线 角平分线所在直线 方程; 方程;
(Ⅲ)在椭圆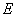 上是否存在关于直线 上是否存在关于直线 对称的相异两点?若存在,请找出;若不存在,说明理由. 对称的相异两点?若存在,请找出;若不存在,说明理由.
解(Ⅰ)易求得椭圆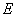 的方程为 的方程为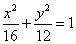 (过程略); (过程略);
(Ⅱ)可求得直线 的方程为 的方程为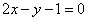 (过程略); (过程略);
(Ⅲ)假设存在这样的两个不同的点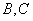 ,设 ,设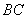 中点为 中点为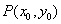 .因为 .因为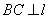 ,所以 ,所以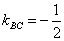 ,又 ,又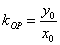 ,由本文性质3.1得, ,由本文性质3.1得, ,即 ,即 ,也就是 ,也就是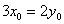 ①,又点 ①,又点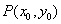 在直线 在直线 上,所以有 上,所以有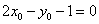 ②,联立①②解得 ②,联立①②解得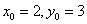 ,所以 ,所以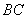 中点就是点 中点就是点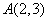 ,因点 ,因点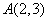 在椭圆上,而弦 在椭圆上,而弦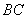 的中点不可能在椭圆上,故不存在关于直线 的中点不可能在椭圆上,故不存在关于直线 对称的相异两点. 对称的相异两点.
参考文献:
邹生书.有心曲线与直径相关的切线性质.河北理科教学研究.2010(5)
(责任编辑:admin)
|