巧设配偶因子证明一类轮换对称不等式
http://www.newdu.com 2025/05/19 02:05:55 人民教育出版社 佚名 参加讨论
巧设配偶因子证明一类轮换对称不等式 湖北省阳新县高级中学 邹生书 笔者经研究发现，有一类轮换对称不等式的证明问题，可通过巧构待定配偶式并运用均值不等式的方法进行证明．该证法可操作性强易于掌握，现结合典型例题介绍如下． 例1（第19届北欧竞赛题）设  是正实数，求证： ．证明：令  ，由均值不等式得 ，此不等式等号成立条件是 即 ．又易知所证不等式等号成立的条件是 ，此时 ．于是有 ，同理有 ， ，将这三个不等式相加化简即得所证不等式．例2 设 是正实数，且 ，求证： ．证明：令 ，由均值不等式得 ，此不等式等号成立条件是 即 ．又易知所证不等式等号成立的条件是 ，此时 ．于是有 ，同理有 ， ，将这三个不等式相加得， ．又由均值不等式可得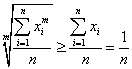，  ，代入上式得所证不等式．例3若  为小于1的正数且 ， 且 ，则 ．证明：因  ，则 ．令，由均值不等式得 ，此不等式等号成立的条件是 ，即 ．又易知所证不等式等号成立的条件是 ，此时 ，于是有 ，即 ，其中 ，将这 个不等式相加得， ．因为  ，所以 ，即 ，代入上述不等式化简得： ，即．注：在例1中，当  时就是下列命题： 若为小于1的正数且，则 ．例4（1984年巴尔干地区数学竞赛题）设  且 ，求证： ．证明：所证不等式即 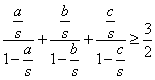 ，也就是 ，亦即 ，也就是 ，故只需证 ．构造  ，此不等式等号成立的条件是 ，即 ．又易知所证不等式等号成立的条件是 ，此时 ，于是有 ，即 ，其中．将这个不等式相加得， ，把代入得，故原不等式成立．例5 已知  ，求证： ．证明：设  ，则所证不等式可化为 ，进而变为 ，再令 ，则 且 ，所证不等式变为 ，分离常数得 ．构造  ，则此不等式等号成立的条件是 ，即 ．又易知所证不等式等号成立的条件是 ，此时 ，所以 ，即 ，同理可得 ， ，将这三个不等式相加得， ，又，所以，故原不等式成立．本文充分利用轮换对称不等式的结构特点以及等号成立的条件为导向，运用待定系数法构造配偶式，然后运用均值不等式等号成立的条件以及所证轮换对称不等式等号成立的条件求出待定系数，从而使所证不等式获得证明．其中设配偶式求配偶因子是该证法的关键一步和核心部分． (责任编辑：admin) |