有关对称问题的求法小结
河南省周口市淮阳县第一高级中学数学组 张明选
摘 要:对称问题是高中数学的一个重要知识点,部分题目还会涉及光线反射等一些实际的应用,有关对称问题的求解,除了初中时期学习的数形结合的方法外,高中学习过直线方程后,更明了了其理论基础,本文,我从对称的理论原理出发探讨对称问题的具体求解方法。
关键词:中点坐标;斜率;交点坐标;对称
对称问题是高中数学的一个重要知识点,是学生的学习难点,也是不少教师的教学难点。高中数学中所涉及到的对称问题主要包括:点关于点的对称,点关于直线的对称,直线关于直线的对称。这里我就这三种对称关系的求法给以总结,以便我们能够系统理解有关对称问题的具体求法。
一、点关于点的对称
大家应该很熟悉平面直角坐标系中的一个点 关于原点对称的点 关于原点对称的点 的坐标写法,即将点 的坐标写法,即将点 的横纵坐标都变为他们的相反数即可。这种做法在初中的时候很多老师就要求学生记忆过,但是其理论基础是高中学习的中点坐标公式,我们也正是利用中点坐标公式来解决任意两点(不单单是关于原点)的对称问题。 的横纵坐标都变为他们的相反数即可。这种做法在初中的时候很多老师就要求学生记忆过,但是其理论基础是高中学习的中点坐标公式,我们也正是利用中点坐标公式来解决任意两点(不单单是关于原点)的对称问题。
例1 设点 ,求点 ,求点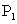 关于点 关于点 对称的点 对称的点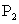 的坐标. 的坐标.
分析:当点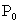 是坐标原点时,我们可以直接写出点 是坐标原点时,我们可以直接写出点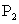 的坐标为 的坐标为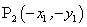 ,但是对于任意的点 ,但是对于任意的点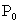 我们就不能直接写出对称点 我们就不能直接写出对称点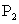 的坐标,而必须利用中点坐标公式. 的坐标,而必须利用中点坐标公式.
解:设点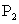 的坐标是 的坐标是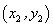 ,由于 ,由于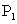 与 与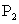 关于点 关于点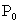 对称,因此点 对称,因此点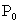 是 是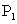 与 与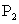 两点的中点,所以有 两点的中点,所以有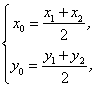 解得 解得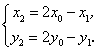
对称点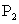 的坐标是 的坐标是 . .
二、点关于直线的对称
根据数形结合的思想,我们知道点关于坐标轴对称的求法,甚至我们知道一个点关于一特殊的直线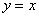 的对称的点坐标的写法,给定一个点 的对称的点坐标的写法,给定一个点 ,则它关于直线 ,则它关于直线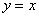 对称的点 对称的点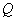 的坐标是 的坐标是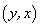 .但是当这一特殊的直线(坐标轴和 .但是当这一特殊的直线(坐标轴和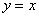 直线)变为一般的直线时,点关于直线的坐标的求法就要利用高中阶段学习的两直线垂直时的斜率关系式,以及点与直线的位置关系方程.其实这也正是点关于特殊直线对称的理论基础. 直线)变为一般的直线时,点关于直线的坐标的求法就要利用高中阶段学习的两直线垂直时的斜率关系式,以及点与直线的位置关系方程.其实这也正是点关于特殊直线对称的理论基础.
我们假设已知点 的坐标是 的坐标是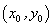 ,已知直线方程(非坐标轴直线)是 ,已知直线方程(非坐标轴直线)是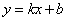 ,求点 ,求点 关于已知直线的对称点 关于已知直线的对称点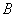 的坐标. 设对称点 的坐标. 设对称点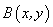 ,我们只需求出 ,我们只需求出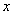 和 和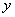 的值即可.点 的值即可.点 与点 与点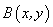 关于直线 关于直线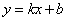 对称,那么直线必垂直平分线段 对称,那么直线必垂直平分线段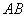 ,所以有以下两点:线段 ,所以有以下两点:线段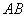 的中点在直线上; 的中点在直线上;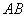 所在的直线与直线 所在的直线与直线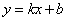 相互垂直。根据中点坐标公式线段 相互垂直。根据中点坐标公式线段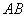 的中点 的中点 在直线 在直线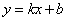 上,点 上,点 就要满足直线方程,即 就要满足直线方程,即 . .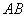 所在的直线的斜率 所在的直线的斜率 ,根据两直线垂直的关系:斜率的乘积等于 ,根据两直线垂直的关系:斜率的乘积等于 ,有 ,有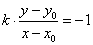 . .
综上我们有以下方程组:
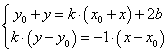
上述方程组中只有未知量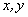 ,解此方程组可得点 ,解此方程组可得点 关于已知直线 关于已知直线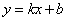 的对称点 的对称点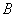 的坐标. 的坐标.
例2 已知点 ,求点 ,求点 关于直线 关于直线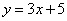 的对称点点 的对称点点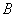 的坐标. 的坐标.
分析:这是一个点关于直线对称的求解问题,针对这类问题,我们只需利用上文分析的中点与直线的关系和两直线的斜率关系即可.求解上述方程组就可以得到对称点的坐标.
解:设点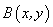 ,点 ,点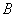 与点 与点 关于直线 关于直线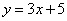 对称,则我们有 对称,则我们有
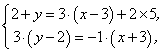 即 即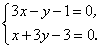
解得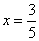 , ,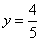 .所以点 .所以点 关于直线 关于直线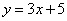 的对称点点 的对称点点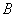 的坐标是 的坐标是 . .
三、直线关于直线的对称
直线关于直线的对称是以点关于直线的对称为基础的,其求解方法及求解的理论基础相同。但是直线关于直线的对称根据两直线的位置关系涉及到了两种不同的情况:当两直线平行时,对称直线的求法;当两直线相交时对称直线的求法。并且直线关于坐标轴的对称直线的求法也可以归结到一般方法之中.
已知直线 与直线 与直线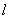 的方程,求直线 的方程,求直线 关于直线 关于直线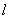 对称的直线 对称的直线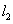 的方程. 的方程.
1.当两直线平行时
直线 与直线 与直线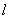 平行,他们的斜率一定相等,设 平行,他们的斜率一定相等,设 : :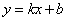 , ,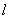 : :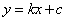 .( .( )直线 )直线 与直线 与直线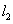 关于直线 关于直线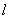 对称,此时两直线一定分布于直线 对称,此时两直线一定分布于直线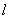 的两侧,且直线 的两侧,且直线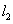 的斜率也是 的斜率也是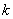 ,所以我们设 ,所以我们设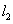 : :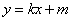 ,我们只需求出截距 ,我们只需求出截距 即可得对称直线的方程.此时可以在已知直线 即可得对称直线的方程.此时可以在已知直线 上任取一点 上任取一点 (为计算方便,我们一般取 (为计算方便,我们一般取 上的特殊点,例如 上的特殊点,例如 与坐标轴的交点),计算点 与坐标轴的交点),计算点 关于直线 关于直线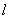 的对称点 的对称点 的坐标(利用上文中点关于直线对称的求法),那么点 的坐标(利用上文中点关于直线对称的求法),那么点 一定在直线 一定在直线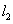 : :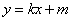 上,将求出的点 上,将求出的点 的坐标代入直线 的坐标代入直线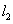 的方程即可得到截距 的方程即可得到截距 的值,同时也就求得了对称直线 的值,同时也就求得了对称直线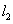 的方程. 的方程.
例3 已知直线 : : ,直线 ,直线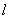 : :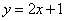 ,求直线 ,求直线 关于直线 关于直线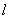 对称的直线 对称的直线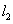 的方程. 的方程.
分析:此题即是两平行直线的对称问题,求解思路是根据斜率直接设出对称直线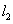 的方程是 的方程是 ,再根据上述分析求 ,再根据上述分析求 得值即可. 得值即可.
解:设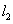 : : ,任取直线 ,任取直线 上一点 上一点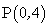 ,(即取直线 ,(即取直线 与 与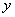 轴的交点坐标),设点 轴的交点坐标),设点 关于直线 关于直线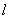 的对称点 的对称点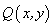 ,则有 ,则有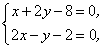
解得点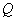 的坐标是 的坐标是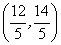 ,而点 ,而点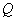 满足直线 满足直线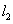 : : ,所以有 ,所以有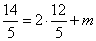
解得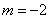 ,所以对称直线 ,所以对称直线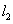 的方程是 的方程是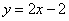 . .
特点总结:直线 与 与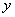 轴的交点坐标与其对称直线 轴的交点坐标与其对称直线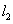 与 与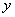 轴的交点坐标的中点坐标恰是直线 轴的交点坐标的中点坐标恰是直线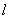 与 与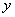 轴的交点坐标,这是巧合吗?不是。当遇两平行直线的对称问题时可以此方法验证解答的正确性。对做选择题、填空题尤其方便快速。 轴的交点坐标,这是巧合吗?不是。当遇两平行直线的对称问题时可以此方法验证解答的正确性。对做选择题、填空题尤其方便快速。
2.当两直线相交时
直线 与直线 与直线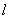 时两相交的直线,则他们必定有交点,求直线 时两相交的直线,则他们必定有交点,求直线 关于直线 关于直线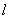 的对称直线 的对称直线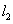 的方程的方法:先求两直线 的方程的方法:先求两直线 与 与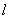 的交点坐标 的交点坐标 ,那么直线 ,那么直线 的对称直线 的对称直线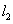 必定经过交点 必定经过交点 ;再在已知直线 ;再在已知直线 上任取一点 上任取一点 (为计算方便,我们一般取 (为计算方便,我们一般取 上的特殊点,例如 上的特殊点,例如 与坐标轴的交点),利用上文点关于直线对称的方法求点 与坐标轴的交点),利用上文点关于直线对称的方法求点 关于直线 关于直线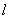 的对称点 的对称点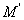 的坐标,则点 的坐标,则点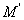 必满足直线 必满足直线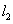 的方程,即点 的方程,即点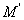 在直线 在直线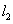 上,这样直线 上,这样直线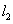 上就有两个确定的点坐标点 上就有两个确定的点坐标点 和点 和点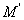 ;最后根据直线的两点式可以写出对称直线 ;最后根据直线的两点式可以写出对称直线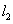 的直线方程.这里不再举例说明,其计算方法与上文类似,主要过程在于点关于直线对称的求法.综合直线关于直线对称的两种情况,我们知道,直线间的对称问题都是以点关于直线的对称问题的基础的,所以我们学习的重点应该是点关于直线的对称的求解方法,结合高中阶段直线部分的一些知识点熟练掌握对称关系的求解方法。 的直线方程.这里不再举例说明,其计算方法与上文类似,主要过程在于点关于直线对称的求法.综合直线关于直线对称的两种情况,我们知道,直线间的对称问题都是以点关于直线的对称问题的基础的,所以我们学习的重点应该是点关于直线的对称的求解方法,结合高中阶段直线部分的一些知识点熟练掌握对称关系的求解方法。
本文主要介绍了高中阶段几种有关对称问题的求解方法,包括:点关于点的对称,点关于直线的对称,直线关于直线的对称三个方面,希望通过本文能够使大家系统了解有关对称问题的求解方法与分析步骤,并掌握其理论基础,有助于今后的学习。
(责任编辑:admin)
|
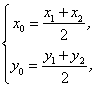 解得
解得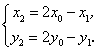
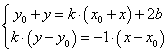
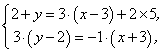 即
即