分式函数值域解法探析
http://www.newdu.com 2025/12/22 10:12:58 人民教育出版社 佚名 参加讨论
分式函数值域解法探析 甘肃省定西工贸中专文峰分校 张占荣 函数既是中学数学各骨干知识的交汇点,是数学思想,数学方法应用的载体,是初等数学与高等数学的衔接点,还是中学数学联系实际的切入点,因此函数便理所当然地成为了历年高考的重点与热点,考查函数的定义域、值域、单调性、奇偶性、反函数以及函数图象。而对函数值域的考查或是单题形式出现,但更多的是以解题的一个环节形式出现,其中求分式函数的值域更是学生失分较大知识点之一。为此,如何提高学生求分式函数值域的能力,是函数教学和复习中较为重要的一环,值得探讨。下面就本人对分式函数值域的教学作如下探究,不馁之处、敬请同仁指教。 一、相关概念 函数值是指在函数y=f(x)中,与自变量x的值对应的y值。 函数的值域是函数值的集合,是指图象在y轴上的投影所覆盖的实数y的集合。函数的值域由函数的定义域及其对应法则唯一确定;当函数由实际问题给出时,函数的值域由问题的实际意义确定。 分式函数是指函数解析式为分式形式的函数。 二、分式函数的类型及值域解法 类型一:一次分式型 一次分式型是指分子与分母都是关于自变量x(或参数)的一次函数的分式函数。 1.y= 例1 求函数y= 解法一:常数分离法。将y= 解:∵y= ∴y 解法二:反函数法。利用函数和它的反函数的定义域与值域的互逆关系,通过求反函数的定义域,得到原函数的值域。 解:反解y= 对调 y= ∴函数y= 2.y= 分析:这是一道含三角函数的一次分式函数,由于含三角函数,不易直接解出x,但其有一个特点:只出现一种三角函数名。可以考虑借助三角函数值域解题,其实质跟y= 即:将y= 例2 求函数y= 解:由y= ∵ -1≤sinx≤1, ∴-1≤ 解之得 3.y= 分析:这道题不仅含有三角函数,且三角函数不同,例2解法行不通,但反解之后会出现正、余弦的和、差形式,故可考虑用叠加法。 即:去分母以后,利用叠加公式和|sinx|≤1解题。 例3 求函数y= 解:∵2cosx+10 ∴3sinx-2ycosx=10y+3。 ∴ 由 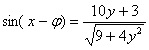 和 和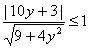 , ,∴ ∴ 总结:求一次分式函数的值域,首先要看清楚是在整个定义域内,还是在指定区间上;其次用反函数法解题;再次还要注意含三角函数的分式函数,其实质是在指定区间上求分式函数的值域。 类型二:二次分式型 二次分式型是指分子与分母的最高次项至少有一项是关于x的二次函数。由于出现了x2项,直接反解x的方法行不通。但我们知道,不等式、函数、方程三者相互联系,可以相互转化。所以可考虑将其转化为不等式或方程来解题。 1.y= 分析:去分母后,可将方程看作是含参数y的二次方程f(x)=0。由于函数的定义域并非空集,所以方程一定有解, 即:用判别式法。先去分母,得到含参数y的二次方程f(x)=0,根据判别式 例4 求函数y= 解:由y= 当y=0时,x=0,当y≠0时,由△≥0得- ∵函数定义域为R, ∴函数y= 说明:判别式法求二次函数的值域只适用于在整个定义域内,但不能用其在指定的区间上求二次函数的值域,否则就会放大值域。 2.y= 例5 求 分析:因为x< 解:∵x< ∴ =[(5-4x)+ ≥2 =-2, ∴原函数的值域为 例6 求 错解: 分析:在使用均值定理时一定要注意使用条件“一定、二正、三相等”,显然上述解法中 解:用单调性法 令 任取2≤t1≤t2,则f(t1)= t1+ f(t1)- f(t2)=( t1+ ∵2≤t1≤t2 ∴t1- t2<0, t1· t2≥4, 1- ∴f(t1)- f(t2)=( t1- t2)( 1- ∴f(t1)< f(t2),即函数y=t+ ∴当t=2、即 ∴原函数的值域为 总结:不管是求一次分式函数,还是求二次分式函数的值域,都必须注意自变量的取值范围。虽然我们提倡通解通法的培养,但一定要看到只有对一类题才可以用通解通法。若失去同一类前提,只强调通解通法,便是空中楼阁。 故要因题而论,就事论事,防止一概而论的错误,用辩证和发展的眼光看待问题,这样才会起到事半功倍的效果。 三、提炼知识,总结分式函数值域解法 求函数的值域是高中数学的难点之一,它没有固定的方法和模式。但我们可以针对不同的题型进行归类总结,尽最大可能地寻找不同类型分式函数求值域的通解通法。常用的方法有: 1.反函数法。反函数法是求一次分式函数的基本方法,是利用函数和它的反函数的定义域与值域的互逆关系,通过求反函数的定义域,得到原函数的值域。但要注意看清楚是在整个定义域内,还是在指定区间上求值域。 2.判别式法。判别式法是求二次分式函数的基本方法之一,即先去分母,把函数转化成关于x的二次方程f(x,y)=0,因为方程有实根,所以判别式△≥0,通过解不等式求得原函数的值域。需注意的是判别式法求二次函数的值域只适用于在整个定义域内。 3.不等式法。不等式法是利用基本不等式:a+b≥2 4.换元法。换元法是求复合型分式函数值域的常用方法。当分式函数的分子或分母出现子函数(如三角函数)时,可考虑用换元法,将所给函数化成值域容易确定的另一函数,从而求得原函数的值域。要注意换元后自变量的取值范围。 5.单调性法。单调性法是通过确定函数在定义域(或某个定义域的子集)上的单调性求出函数的值域的方法。 另外,还可以根据函数的特点,利用数形结合或求导数的方法求分式函数的值域。由于这些方法不是很常用,在此就不多做说明。 (责任编辑:admin) |