椭圆与双曲线的对偶性质之椭圆篇(2)
杨志明
21.若P为椭圆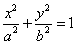 (a>b>0)上异于长轴端点的任一点,F1, F 2是焦点, (a>b>0)上异于长轴端点的任一点,F1, F 2是焦点, 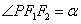 , , 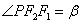 ,则 ,则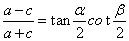 . .
22.椭圆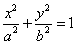 (a>b>0)的焦半径公式: (a>b>0)的焦半径公式:
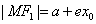 , ,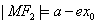 ( (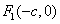 , , 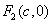 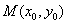 ). ).
23.若椭圆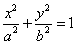 (a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当 (a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当
0<e≤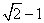 时,可在椭圆上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项. 时,可在椭圆上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
24.P为椭圆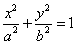 (a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则 (a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则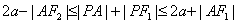 ,当且仅当 ,当且仅当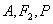 三点共线时,等号成立. 三点共线时,等号成立.
25.椭圆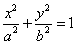 (a>b>0)上存在两点关于直线 (a>b>0)上存在两点关于直线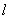 : :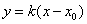 对称的充要条件是 对称的充要条件是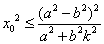 . .
26.过椭圆焦半径的端点作椭圆的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.
27.过椭圆焦半径的端点作椭圆的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.
28.P是椭圆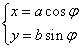 (a>b>0)上一点,则点P对椭圆两焦点张直角的充要条件是 (a>b>0)上一点,则点P对椭圆两焦点张直角的充要条件是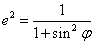 . .
29.设A,B为椭圆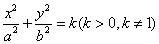 上两点,其直线AB与椭圆 上两点,其直线AB与椭圆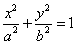 相交于 相交于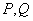 ,则 ,则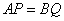 . .
30.在椭圆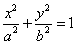 中,定长为2m(o<m≤a)的弦中点轨迹方程为 中,定长为2m(o<m≤a)的弦中点轨迹方程为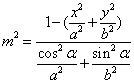 ,其中 ,其中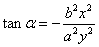 ,当 ,当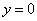 时, 时, 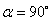 . .
31.设S为椭圆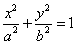 (a>b>0)的通径,定长线段L的两端点A,B在椭圆上移动,记|AB|= (a>b>0)的通径,定长线段L的两端点A,B在椭圆上移动,记|AB|=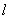 , ,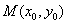 是AB中点,则当 是AB中点,则当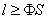 时,有 时,有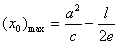 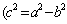 , ,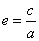 );当 );当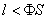 时,有 时,有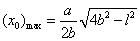 , ,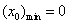 . .
32.椭圆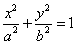 与直线 与直线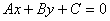 有公共点的充要条件是 有公共点的充要条件是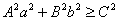 . .
33.椭圆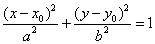 与直线 与直线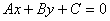 有公共点的充要条件是 有公共点的充要条件是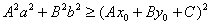 . .
34.设椭圆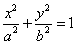 (a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记 (a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记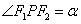 , , 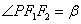 , ,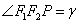 ,则有 ,则有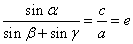 . .
35.经过椭圆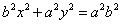 (a>b>0)的长轴的两端点A1和A2的切线,与椭圆上任一点的切线相交于P1和P2,则 (a>b>0)的长轴的两端点A1和A2的切线,与椭圆上任一点的切线相交于P1和P2,则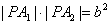 . .
36.已知椭圆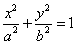 (a>b>0),O为坐标原点,P、Q为椭圆上两动点,且 (a>b>0),O为坐标原点,P、Q为椭圆上两动点,且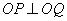 .(1) .(1)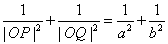 ;(2)|OP|2+|OQ|2的最大值为 ;(2)|OP|2+|OQ|2的最大值为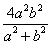 ;(3) ;(3)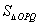 的最小值是 的最小值是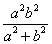 . .
37.MN是经过椭圆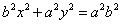 (a>b>0)过焦点的任一弦,若AB是经过椭圆中心O且平行于MN的弦,则 (a>b>0)过焦点的任一弦,若AB是经过椭圆中心O且平行于MN的弦,则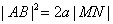 . .
38.MN是经过椭圆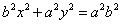 (a>b>0)焦点的任一弦,若过椭圆中心O的半弦 (a>b>0)焦点的任一弦,若过椭圆中心O的半弦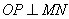 ,则 ,则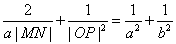 . .
39.设椭圆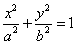 (a>b>0),M(m,o) 或(o, m)为其对称轴上除中心,顶点外的任一点,过M引一条直线与椭圆相交于P、Q两点,则直线A1P、A2Q(A1 ,A2为对称轴上的两顶点)的交点N在直线 (a>b>0),M(m,o) 或(o, m)为其对称轴上除中心,顶点外的任一点,过M引一条直线与椭圆相交于P、Q两点,则直线A1P、A2Q(A1 ,A2为对称轴上的两顶点)的交点N在直线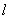 : :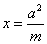 (或 (或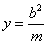 )上. )上.
40.设过椭圆焦点F作直线与椭圆相交 P、Q两点,A为椭圆长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的椭圆准线于M、N两点,则MF⊥NF.
(责任编辑:admin)
|
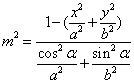 ,其中
,其中