学好几何符号语言
http://www.newdu.com 2024/12/03 08:12:35 人民教育出版社 佚名 参加讨论
学好几何符号语言 数学的说理性很强，因此用文字语言来叙述说理过程时，写的人嫌麻烦，读的人又觉得累赘，写和读的人都跟不上思考，常常迫使思路中断。为了简化叙述，自古至今数学家们努力创造了大量缩写符号，简化叙述，使解决问题的思路顺畅。代数的符号率先出现，最早使用数学符号的是公元3世纪的数学家丢番图。随着科学的迅速发展，作为科学公仆的数学迫切需要改进表述方式方法，于是现代数学的符号体系开始在欧洲形成了。 许多数学符号很形象，一看就明了它的含意。如第一个使用现代符号“＝”的数学家雷科德就这样说道：“再也没有别的东西比它们更相等了。”他的巧妙构思得到了公认，从而相等符号“＝”沿用了下来。 最灿烂而美丽的图形科学──几何，为了进一步发展，许多几何符号应运而生。如平行符号“∥”多么简单又形象，给人们抽象而丰富的想象，在同一个平面内的两条线段各自向两方无限延长，它们永不相交，揭示了两条直线平行的本质。 数学符号有两个基本功能，一是准确、明了地使别人知道指的是什么概念，二是书写简便。自觉地引入符号体系的是法国数学家韦达（1854—1603年），而现代数学符号体系却采取笛卡儿（1596—1650年）使用的符号，欧拉（1707一1783）为符号正规化工作作出不少贡献。如用a、b、c表示三角形ABC的三边等等，都应归功于欧拉。 数学中的符号越来越多，往往被人们错误地认为数学是一门难懂而又神秘的科学。当然，如果不了解数学符号含意的人就看不a懂大量天书般符号的数学，唯有进了数学大门才能真正发觉数学符号给数学理论的表达和说理带来莫大的方便，甚至感到是必不可少的。说来也奇怪，地球上不同地区采用不同的文字，可是数学符号却成了世界通用语言。因此为了学好几何，必须加强几何符号语言的训练。 第一，彻底理解每一个几何符号的含意 例如符号A、B、C......没有什么几何意义，只有分别在它们前面或后面写上“点”字，才表示图1中的点。又如AB前面写上“直线”“线段”或“射线”，就分别表示图2中（a）、(b）、（c）的几何图形，否则符号AB就表示线段AB的长度，是一个数，因此3AB和  AB分别表示线段AB长度的三倍和三分之一。 再如符号∠ABC和△ABC表示不同的几何图形，前者是角（图（3a）），后者是三角形（图（3b））。 显然，要真正了解一个几何符号，必须首先理解相应的几何概念。  第二，正确书写几何符号。 数学符号大多是经过长期发展而形成的。有些数学事实曾经有过五花八门的符号，如减号，数学家丢番都用符号“↑”表示，后人又用字母m（minus）表示，到15世纪才确认用符号“-”表示。因此，一个好的数学符号经历了适者生存的规律的考验。对这些数学符号（包括几何符号）都要严格按标准书写，书写几何符号是叫人容易看懂，不是叫人去猜谜语。 第三，不能臆造几何符号。 通行的几何符号已经得到了人们的公认，成了世界通用的符号，一般是不能随意变动的。对于没有的符号也不能随便臆造，如“∠”表示锐角，  表示钝角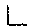，“ ”表示直角，似乎很有意义，然而真正用起来就会发生许多不便，说明了这种符号的引人没有必要，也不可行。不要臆造新的几何符号，并不是要大家墨守成规，不要创新。事实上，新的数学知识产生，必然有新的符号出现。大科学家爱因斯坦在他的遗稿中就有不少新的符号，至今尚未破译，不知道他说些什么，如果他生前公布了他研究的新成果，说不定这些符号也就此出世了。但是，作为学生不要想入非非，重要的是要打好基础。 最后，我们再谈谈几何文字语言、几问图形语言和几何符号语言三者的关系。这三种语言都是几何语言，在学习或研究几何中都很重要，缺一不可，因此就存在着它们间“互译”的问题。例如，“读下列语句，并画出它们的图形：直线a、b相交于点C，直线b、c相交于点A，直线a、c相交于点B。这时我们说‘直线a、b、c两两相交‘。”此题要求我们把几何文字语言“翻译”成几何图形语言，如果“翻译”（画）成图4就错了，因为题中a虽然出现两次（“直线a、c相交”和“直线a、b相交”），可是都在同一道题中，所以在图中只能出现一次。至于直线b、c同样如此，分别在图中只允许出现一次。正确的“翻译”（画法）应是图5。   只有正确理解它们，才能进行正确互译。 (责任编辑：admin) |
- 上一篇：容易混淆的数学概念（三）
- 下一篇：比算术方法好(二)