陈子测日与勾股定理之发现
http://www.newdu.com 2025/09/08 07:09:54 人民教育出版社 佚名 参加讨论
陈子测日与勾股定理之发现 太阳距离我们有多远呢?这对于近代人来说,是一个常识性的问题;但对古代人而言,它却是个谜。为了解开这个谜,古代科学家进行了一次又一次探测。 据公元前一世纪成书的《周髀算经》记载,我国古代杰出的数学家陈子(公元前6-7世纪)对太阳的高和远进行了测量,这就是人们所乐于称道的“陈子测日”。他的测量方法原理如图1所示。 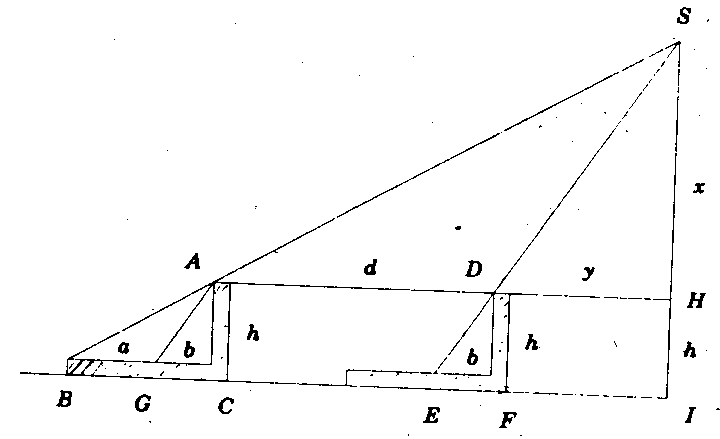 图 1 其中,S表示太阳,I表示日下点,AC和DF均表示髀,即测量用的标杆。C、F、I在同一直线上。b是髀竖立在F处的影长,a+b是髀竖立在C处的影长。髀长h是已知的,a、b、d均可实际量出。 由 △SHD∽△ACG, △SDA∽△AGB, 有  于是,便可求出太阳S到日下点I的距离,即日高SI;并且,还可求出髀DF到太阳日下点I的距离FI。但是,由陈子受当时科学水平的限制,误把椭球形的地球当作平面。所以,求出的日高与实际距离相差很远。然而,他的测日法所反映的数学及测量水平却是在世界上遥遥领先的,而且他的测量方法(后来叫做重差术)至今仍被使用着。所以,人们称陈子为测量学之祖,毫不为过。 求得了日高及髀到日下点的距离之后,髀到太阳的距离即日远,陈子是怎样计算的呢?据《周髀算经》记载,有一次荣方和陈子问答,陈子说:“若求邪至日者,以日下为勾,日高为股,勾股各自乘,并开方而除之,得邪至日者。”(古汉语“邪”也作“斜”解)就是说,将勾、股各平方后相加,再开方,就得到弦长(图2)。陈子的这段话,不仅解决了日远的计算问题,而且还最早表述了勾股定理。这充分证明,我国至迟在陈子所处年代,已经发现并运用了勾股定理。  图 2 可是,你是否想到过,我们的祖先发现勾股定理,不是一赋而就,而是经历了漫长的岁月,走过了一个由特殊到一般的过程。 我国的几何起源很早。据考古发现,十万年前的“河套人”就已在骨器上刻有菱形的花纹;六、七千年前的陶器上已有平行线、折线、三角形、长方形、菱形、圆等几何图形。随着生活和生产的需要,越来越多的几何问题摆在我们祖先面前。四千年前,黄河流域经常洪水泛滥。大禹(公元前二十一世纪)率众治水,开山修渠,导水东流。在治水过程中,他“左准绳,右规矩”。(这里“规”就是圆规,“矩”就是曲尺,由长短两尺在端部相交成直角合成,短尺叫勾,长尺叫股),运用勾股测量术进行测量。在《周髀算经》中,表明大禹已经知道用长为3:4:5的边构成直角三角形。 到了商高(公元前1120年)所处时代,我国的测量技术及几何水平达到了一定高度。《周髀算经》中,记载着周公与商高的一段对话,商高说:“故折矩以为勾广三,股修四,径隅五。”这里的“勾广”就是勾长,“股修”就是股长,“径隅”就是弦长。就是说,把一根直尺折成矩(直角),如果勾长为3,股长为4,那么尺的两端间的距离,即弦长必定是5。这表明,早在三千年前,我们的祖先就已经知道“勾三股四弦五”这一勾股定理的特例了。 从制作工具、测量土地山河,到研究天文;从大禹治水,到陈子测日,我们的祖先逐渐积累经验,从而发现了勾股定理。为纪念我们祖先的伟大成就,我国已将这个定理命名为勾股定理。 尽管希腊人称勾股定理为毕达哥拉斯定理或“百牛定理”,法国、比利时人又称这个定理为“驴桥定理”,但据推算,他们发现勾股定理的时间都比我国晚。我国是世界上最早发现勾股定理这一几何宝藏的国家! (责任编辑:admin) |