数学与音乐
http://www.newdu.com 2025/09/09 01:09:11 人民教育出版社 佚名 参加讨论
数学与音乐 难道不可以把音乐描述为感觉的数学,把数学描述为理智的音乐吗? ──J.J.西尔威斯特 若干世纪以来,音乐和数学一直被联系在一起。在中世纪时期,算术、几何、天文和音乐都包括在教育课程之中。今天的新式计算机正在使这条纽带绵延不断。  乐谱的书写是表现数学对音乐的影响的第一个显著的领域。在乐稿上,我们看到速度、节拍(4/4拍、3/4拍,等等)、全音符、二分音符、四分音符、八分音符、十六分音符,等等。书写乐谱时确定每小节内的某分音符数,与求公分母的过程相似──不同长度的音符必须与某一节拍所规定的小节相适应。作曲家创作的音乐是在书写出的乐谱的严密结构中非常美丽而又毫不费力地融为一体的。如果将一件完成了的作品加以分析,可见每一小节都使用不同长度的音符构成规定的拍数。  除了数学与乐谱的明显关系外,音乐还与比率、指数曲线、周期函数和计算机科学相联系。 毕达哥拉斯学派(公元前585~前400)是最先用比率将音乐与数学联系起来的。他们认识到拨动琴弦所产生的声音与琴弦长度有关,从而发现了和声与整数的关系。他们还发现谐声是由长度成整数比的同样绷紧的弦发出的──事实上被拨弦的每一和谐组合可表示成整数比。按整数比增加弦的长度,能产生整个音阶。例如,从产生音符C的弦开始,C的16/15长度给出B,C的6/5长度给出A,C的4/3长度给出G,C的3/2长度给出F,C的8/5长度给出E,C的16/9长度给出D,C的2/1长度给出低音C。 你是否曾对大型钢琴为何制作成那种形状表示过疑问?实际上许多乐器的形状和结构与各种数学概念有关。指数函数和指数曲线就是这样的概念。指数曲线由具有y=kx形式的方程描述,式中k>0。一个例子是y=2x。它的坐标图如下。  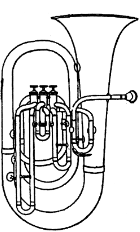 不管是弦乐器还是由空气柱发声的管乐器,它们的结构都反映出一条指数曲线的形状。 19世纪数学家约翰·傅里叶的工作使乐声性质的研究达到顶点。他证明所有乐声──器乐和声乐──都可用数学式来描述,这些数学式是简单的周期正弦函数的和。每一个声音有三个性质,即音高、音量和音质,将它与其他乐声区别开来。 傅里叶的发现使声音的这三个性质可以在图形上清楚地表示出来。音高与曲线的频率有关,音量和音质分别与周期函数①的振幅和形状有关。 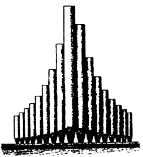 如果不了解音乐的数学,在计算机对于音乐创作和乐器设计的应用方面就不可能有进展。数学发现,具体地说即周期函数,在乐器的现代设计和声控计算机的设计方面是必不可少的。许多乐器制造者把他们的产品的周期声音曲线与这些乐器的理想曲线相比较。电子音乐复制的保真度也与周期曲线密切相关。音乐家和数学家将继续在音乐的产生和复制方面发挥同等重要的作用。 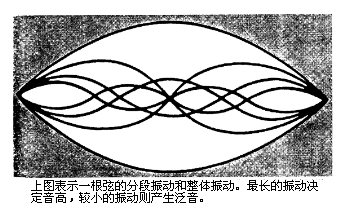 上图表示一根弦的分段振动和整体振动。最长的振动决定音高,较小的振动则产生泛音。 ①周期函数即以等长区间重复着形状的函数。 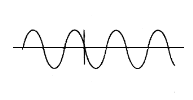 (责任编辑:admin) |