用数学注释的花园
http://www.newdu.com 2025/09/10 09:09:39 人民教育出版社 佚名 参加讨论
用数学注释的花园 日出时分,园丁来到她的花园,她呼喊道,“早上好!”她丝毫不知道在叶片和沃土中潜藏着奇怪的东西。作物根部深处有分形和网络,而在大波斯菊、蝴蝶花、金盏花和雏菊里面,斐波那契数正凝视着她。 她像平时一样地照料着她的花园。每到一处,总出现一些不平常的事情,但是她都忽视了,只迷恋于自然界呈现在表面上的美景。 她先去整理她的蕨类植物。她在把枯死的蕨叶除去,使新的提琴状头部露出时,并没有认识到等角螺线正在迎候着她,也没有注意到蕨叶的分形状构造。突然,当微风转向时,她猛然闻到了忍冬花的香气。纵眼望去,她看到它已越过篱笆,伸入豌豆丛中。她断定确实需要将它仔细修剪一番。她不知道螺旋线正在起作用,即呈左手螺旋状的忍冬花藤已经缠绕在呈右手螺旋状的某些豌豆藤上了。需要用手小心地防止它们损坏她新种的豌豆。 接着她来到为了使花园产生一点异国情调而种植的棕榈树下面除草。树枝在微风中摆动,她没有意识到渐伸线正在擦着她的肩头。  她沾沾自喜地望着她的玉米。“哈!”她想。她对种植玉米曾经踌躇过,但终于因玉米幼株长势喜人而决定种植。她不知道玉米粒的三重联结会在玉米穗内形成。 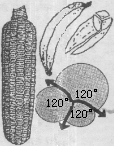 整个花园正在逐渐成形,植物正在茁壮成长,这景况是多么喜人啊!在赞美槭树上新的绿叶时,她知道它们的形状中蕴藏着某种可爱的东西──自然界的对称线是很尽职的。而自然界的叶序则只有受过训练的眼睛才会从萌生在植物枝茎上的叶子中看出。  她举目四顾,把注意力集中在一片胡萝卜土地上。她对胡萝卜的长势感到骄傲,并且注意到需要把它们弄得稀疏些,以保证收获到个头均匀而且大小合宜的胡萝卜。她不想让自然界用胡萝卜来镶嵌空间。 她没有意识到花园中到处是等角螺线。它们存在于雏菊和其他花卉的头状花序之中,许多生长着的东西会形成这种螺线,因为它们长大时要保持形状不变。 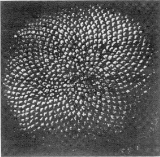 气温渐渐高了,所以她决定在太阳下山时再继续作业。同时她作出一个最后的评价──赞美她用心选择的花卉、菜蔬和其他植物是搭配得如此得当。但是她又一次忽略了什么。她的花园充满着球形、圆锥、多面体和其他几何形状,可是她并未觉察到它们。 当自然界在花园中创造着奇迹时,大多数人对于自然界习以为常的大量计算和数许多对称类型出现在花园内。例如在上图中,人们能在甘蓝小花中找到点对称,在叶中找到线对称。学工作视而不见。自然界清楚地知道如何利用有限的材料和空间工作,并产生出最和谐的形式。因此,在春季的每一天,这位园丁都懵懵懂懂地走进她的领地。她要找出每天给她带来的新的生长和繁盛,却不注意在她的园地里开放着的美丽的数学鲜花。  分形能表现为对称地变化/生长的对象,或随机地非对称地变化的对象。在任一种情形中,分形都是按照用来描述和支配一个初始对象的生长的一些数学规则和模式而变化的。人们把一个几何分形看作无尽的生成模式──不断以较小式样复制自己的模式。于是当一个几何分形的一部分被放大时,它看起来恰如原来的式样。反之,当欧几里得几何对象例如圆的一部分被放大时,它看起来就逐渐地不那么弯曲了。蕨类植物是分形复制的理想例子。如果你瞄准分形蕨的任何部分,它看来就像原来的蕨叶。分形蕨可以在计算机上生成。  网络是把一个问题或状况用较简单的图表现出来的数学图形。网络被欧拉用在柯尼斯堡桥问题中(见本书“数学三剑客──逻辑、娱乐和游戏”章)。他把这问题简化成一个简单的图形,经过分析把它解决了。今天网络是拓扑学中常用的工具。 斐波那契数即 1,1,2,3,5,8,13,21,…。斐波那契(比萨的伦纳多)是中世纪的主要数学家之一。虽然他在算术、代数和几何领域都作出过重大贡献,他在今天则仅因这一数列而闻名,这正是他的《算盘书》(Liber Abaci)中一个难题的解。在19世纪,法国数学家爱德华?卢卡斯编的一本娱乐性数学书中有这个问题。斐波那契的名字与这数列联系起来就在此时。在自然界,这数列出现在下列植物中: ·花瓣数是斐波那契数的花(延龄草、野玫瑰、美洲血根草、大波斯菊、耧斗菜、百合花、蝴蝶花)  ·叶、细枝和茎的排列形式称做叶序。选择茎上一片叶子,从它开始数叶片(假定没有一片折断),直至与所选叶片在同一直线上的叶片为止。数得的叶片数(所选第一片不计)在许多植物中通常是斐波那契数,例如榆树、樱桃树或梨树。  ·松果数:如果数出松果上的左手和右手螺线,这两个数往往是相邻的斐波那契数。对于向日葵和其他花卉的头状花序来说,情况也是如此。菠萝也是一样。观察菠萝的底部,数出由六边形状鳞皮组成的左右螺线数。它们应该是相邻的斐波那契数。  螺线和螺旋线:螺线是出现在自然界许多场所的数学形式,例如提琴头蕨类植物、藤蔓、贝壳、龙卷风、飓风、松果、银河、旋涡的曲线。有平坦螺线、三维螺线、右手和左手螺线、等角螺线、对数螺线、双曲螺线、阿基米德螺线,而螺旋线则是数学所描述的许多螺线类型中的几种。等角螺线出现在自然界的鹦鹉螺壳、向日葵头状花序、圆形织网蛛的网等生长形式中。等角螺线的儿个特性是:螺线切线同螺线半径所形成的角是全等到的(故名等角);以几何速率增大,因此任何半径被螺线分割成的线段形成几何级数;长大时形状不变。 渐伸线:当一根绳正沿着另一曲线(这里是圆)绕上或脱下时,它描出一条渐伸线。渐伸线的形状见于鹰嘴、鲨鱼背鳍和棕榈树悬叶尖端。  三重联结:三重联结是三个线段的交会点,交点处的三个角都是120°。许多自然事件是由于边界或空间利用率所引起的一些限制而产生的。三重联结是某些自然事件所趋向的一个平衡点。除了别的场合以外,三重联结见于肥皂泡群、玉米棒子上谷粒的构成、地面或石块的裂缝。 对称:对称是人们在蝴蝶躯体、叶片形状、人体结构、圆的完美性中看到和感觉到的完全平衡。从数学的观点看来,一个对象被认为具有轴对称的条件是:人们能找到一条线把它分成全同的两部分,如果有可能沿这线折叠,这两部分将互相完全重叠。一个对象具有点对称的条件是:对于一个特定的点,存在着无穷多条这样的对称轴,例如一个圆对它的中心点来说具有点对称。 镶嵌:镶嵌一个平面,就是说能用平坦的拼砖覆盖这个平面,并且拼砖间没有空隙,也不互相交叠,例如用正六边形、正方形或其他形状的拼砖进行的镶嵌。空间的镶嵌或充填则用立方体或截头八面体等三维对象。 (责任编辑:admin) |