数独的候选数法解题技巧
http://www.newdu.com 2025/12/09 05:12:43 人民教育出版社 佚名 参加讨论
数独的候选数法解题技巧 ──隐性三链数删减法 (Hidden Triples) 概说 遇到了高级、困难级的数独谜题,使得唯一候选数法和 隐性唯一候选数法黔驴技穷的时候,就是各种删减法上场的时机了。在各种的删减法中,哪一个要先用 是随个人之喜好的,并无限制。本页介绍的例子当然可用其它删减法完成解题,但还是要以隐性三链数删减法优先啰! 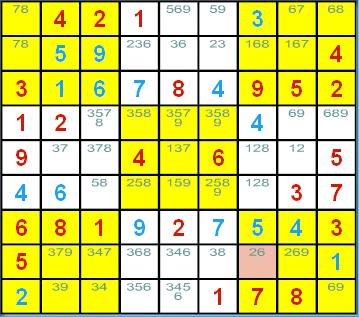 <图 1> 请看<图 1>的第 2 列,数字 1、7、8 只出现在(2, 1)、(2, 7)和(2, 8)这三个宫格的候选数中;这时 隐性三链数删减法的条件已成立了!这表示第 2 列的数字 1、7 和 8 将只能填到这三个宫格中,因为: 如果让别的数字填入这三个宫格之中后,这三个相异的数字能填入的可能宫格就只剩下两个,而那是 不可能的事!所以若这三个宫格的候选数中还有其它数字,全部是多余无用的,它们已不可能再用来 填入这些宫格中了,所以可以毫不考虑的把它们删减掉。于是(2, 7)和(2, 8)这两个宫格候选数中的 6 都可被安全的删减掉;其中(2, 7)的候选数少了数字 6,将使得(8, 7)出现行隐性唯一候选数 6 ,于是 可用隐性唯一候选数法来填入下一个解了。 整理一下: 1. 当某 3 个数字仅出现在某列的某三个宫格候选数中时,就可以把这三个宫格的候选数删减成该 3 个数字。 2. 同理,当某 3 个数字仅出现在某行的某三个宫格候选数中时,就可以把这三个宫格的候选数删减成该 3 个数字。 3. 当然,当某 3 个数字仅出现在某个九宫格的某三个宫格候选数中时,就可以把这三个宫格的候选数删减成该 3 个数字。 利用「找出某 3 个数字仅出现在某行、某列或某一个九宫格的某三个宫格候选数中的情形,进而将这三个 宫格的候选数删减成该 3 个数字」的方法就叫做隐性三链数删减法(Hidden Triples)。 本法其实为隐性数对删除法的推广,而且还可以继续加以推广: 1. 隐性四链数删减法就是:「找出某 4 个数字仅出现在某行、某列或某一个九宫格的某四个宫格候选数中 的情形,进而将这四个宫格的候选数删减成该 4 个数字」的方法。 2. 隐性五链数删减法就是:「找出某 5 个数字仅出现在某行、某列或某一个九宫格的某五个宫格候选数中 的情形,进而将这五个宫格的候选数删减成该 5 个数字」的方法。 3. ...... 如果愿意的话,你确实是可以这样推广的,只是,实用上是否有其应用的价值或空间呢? 隐性三链数删减法示例 隐性三链数删减法一共有 3 种状况:第一种发生在行、第二种是发生在列、第三种则发生在九宫格。<图 1> 就是 发生在列的例子了,其它的情况举例如下: 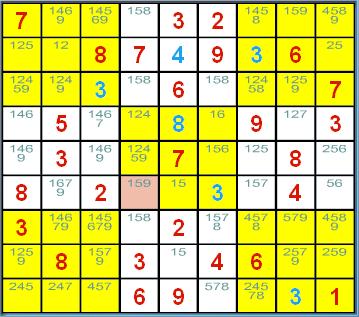 <图 2> <图 2> 是隐性三链数删减发生在行的例子:图中第 4 行的数字 2、4、9 只出现在 (4, 4)、(5, 4)及(6, 4) 这三个宫格的候选数中,所以可以将三个宫格候选数中 2、4、9 以外的数字安全的删减掉,(4, 4)的候选数删减成2、4; (5, 4)的候选数删减成2、4、9;(6, 4)的候选数删减成 9;出现了唯一候选数啦! 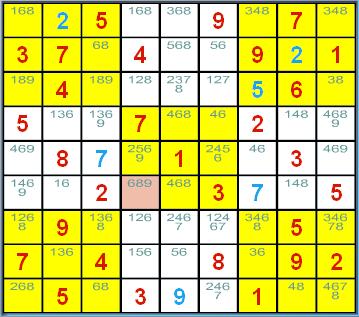 <图 3> <图 3> 是隐性三链数删减发生在九宫格的例子:图中中央九宫格的数字 2、5、9 只出现在 (5, 4)、(5, 6)及(6, 4) 这三个宫格的候选数中,所以可以将三个宫格候选数中 2、5、9 以外的数字安全的删减掉, (5, 4)的候选数删减成2、5、9;(5, 6)的候选数删减成2、5;(6, 4)的候选数删减成 9;出现了唯一候选数啦! 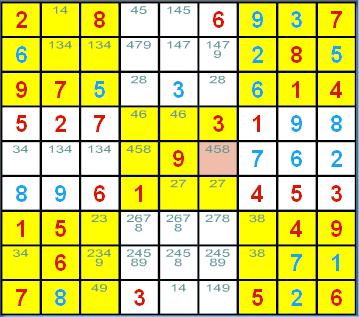 <图 4> 像 <图 1>~<图 3> 这样只经一次删减就出现下一个解的情况当然不错了,但有时可没法这样顺心, <图 4> 就是一个例子。下一个解将出现在(5, 6) 这个宫格,你能找出该填入什么数字吗? 以目前所学到的方法,要解出下一个解,需要二个步骤: 1. 先看中左九宫格吧!由于只剩(5, 1)~(5, 3)这个区块尚未填入数字,所以可用区块删减法将 第 5 列其它区块候选数中的 1、3、4 全部删减掉,但实际上仅能删到(5, 4)及(5, 6)候选数的数字 4 而已。 2. 接下来请观察第 6 行! 由于数字 1、4、9 只出现在 (2, 6)、(8, 6)及(9, 6) 这三个宫格的候选数中 [因为(5, 6)的候选数在上一步骤中已被删减为5、8 了 ], 所以可用隐性三链数删减将三个宫格候选数中 1、4、9 以外的数字安全的删减掉, (2, 6)的候选数删减成1、4、9;(9, 6)的候选数没变;(8, 6)的候选数则由 2、4、5、8、9 删减成 4、9; 由于 5 被删减掉了,使得(5, 6) 出现了行隐性唯一候选数 5 啦! (责任编辑:admin) |