数独的候选数法解题技巧
http://www.newdu.com 2025/12/11 09:12:48 人民教育出版社 佚名 参加讨论
数独的候选数法解题技巧 ──区块删减法 (Single Sector Candidates) 概说 遇到了高级、困难级的数独谜题时,唯一候选数法和 隐性唯一候选数法仍有其黔驴技穷的时候;这时就是区块删减法上场的时机了,往后将要介绍的 数对删减法(Naked Pairs)、隐性数对删减法(Hidden Pairs)、三链数删减法(Naked Triples)、 隐性三链数删减法(Hidden Triples) 、矩形顶点删减法(X-Wing)、三链列删减法(Swordfish)都具有类似的特性:使用这 些技巧的目的仅在删减候选数的数目,删减之后,还是得使用唯一候选数法和隐性唯一候选数法来 找出下一个解并填入数字的。 当使用唯一候选数法或隐性唯一候选数法找不出下一个解时,到底该先使用哪一个删减法呢?随您高兴的用吧! 如果你比较擅长使用数对删减法,那就先用数对删减法吧!如果你认为区块删减法比较好用,那就先用数对删减法吧! ......;介绍时总有先后的次序,但并不表示先介绍的就较好用或必须先用哦!只要能达到:「安全删减掉候选数, 并找出下一个解」的目的,使用哪一种删减法都是可以的。 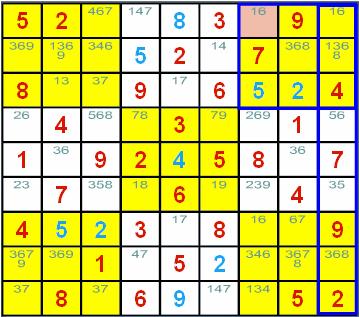 <图 1> 请看<图 1>,这时若使用唯一候选数法或隐性唯一候选数法是找不出下一个解来的!就先来试试区块删减法吧。 请观察第 9 行:数字 1 在本行各宫格的候选数中,是不是仅出现在(1,9)~(3,9)的这一个区块中?太好了,区块删减 的条件已有了;因为这表示第 9 行的数字 1 只能填在(1,9)~(3,9)的这一个区块中,而不论填在本区块 的哪一个宫格中,上右九宫格的其它宫格将因本九宫格已出现数字 1,而不得再填入 1,否则就违反数独填制的规则 啦!所以(1, 7)~(3, 7)及(1, 8)~(3, 8)这两个区块的宫格,如果其候选数中包含有数字 1,就可以毫不考虑的 把它删除掉,因为候选数的意义是可能填入该宫格的数字,而这个数字已不可能再用来填入该宫格中了。啊!太好啦! (1, 7)的候选数中包含有数字 1,所以可以把 (1, 7) 的候选数由 1、6 删减成 6,于是可用唯一候选数法来填入 下一个解了。 当区块删减法的条件成立时,可别高兴得太早,因为很有可能找不到可删减的数字,例如:在<图 1>的第 1 行中, 数字 2 在本行的各宫格候选数中,仅出现在(4, 1)~(6, 1)这一个区块中,而不论数字 2 将来会被填到本区块 的哪一个宫格中,将使得数字 2 不得再填入(4, 2)~(6, 2)及(4, 3)~(6, 3)这两个区块中;但请找找看! 这两个区块各宫格的候选数中全部没有数字 2,所以是白忙了一场,条件是成立了,但候选数并未因此而得到删减。 整理一下,并为了简化叙述起见,下面所述的「区块候选数」表示:该区块的各个宫格候选数的总和。例如(1, 3)~(3, 3) 的区块候选数就是(1, 3)的候选数 4、6、7 及(2, 3)的候选数 3、4、6 及(3, 3)的候选数 3、7 的总和: 3、4、6、7 啦!: 1. 当某一个数字只出现在某行的某一个区块候选数中时,就可以把该数字自包含该区块的九宫格之其它 区块候选数中删减掉。 2. 同理,当某一个数字只出现在某列的某一个区块候选数中时,就可以把该数字自包含该区块的九宫格之其它 区块候选数中删减掉。 3. 同理,当某一个数字只出现在某个九宫格的某一个区块候选数中时,就可以把该数字自包含该区块的行或列之其它 区块候选数中删减掉。 利用「找出某一行、某一列或某一个九宫格各个区块候选数中只出现一次的数字来,并将该数字自包含该区块的另一个 行、列或九宫格的其它区块候选数中删减掉」的方法就叫做区块删减法 (Locked Candidates, Single Sector Candidates)。 区块删减法示例 区块删减法一共有 4 种状况:第一种是发生在行而去删减九宫格、第二种是发生在列而去删减九宫格、 第三种是发生在九宫格而去删减行、第四种是发生在九宫格而去删减列。 <图 1> 就是发生在行而去删减九宫格的例子了,其它的情况举例如下:  <图 2> <图 2> 是发生在列而去删减九宫格的例子:因为第 3 列的数字 6 只出现在 (3, 1)~(3, 3) 这一个区块, 所以可以将上左九宫格的另两个区块 (1, 1)~(1, 3)、(2, 1)~(2, 3) 候选数中的数字 6 安全的删减掉; 于是(1, 1)的候选数 2、6 将被删减成 2,出现了唯一候选数啦!  <图 3> <图 3> 是发生在九宫格而去删减列的例子:因为上右九宫格的数字 5 只出现在 (3, 7)~(3, 9) 这一个区块, 所以可以将第 3 列的另两个区块 (3, 1)~(3, 3)、(3, 4)~(3, 6) 候选数中的数字 5 安全的删减掉; 于是(3, 3)的候选数 5、9 将被删减成 9,出现了唯一候选数啦!  <图 4> <图 4> 是发生在九宫格而去删减行的例子:因为中央九宫格的数字 1 只出现在 (4, 5)~(6, 5) 这一个区块, 所以可以将第 5 行的另两个区块 (1, 5)~(3, 5)、(7, 5)~(9, 5) 候选数中的数字 1 安全的删减掉; 于是(8, 5)的候选数 1、3、7、8 将被删减成 3、7、8;同理,中央九宫格的数字 7、8 都只出现在 (4, 5)~(6, 6) 这一个区块,所以可以将第 5 行的另两个区块 (1, 5)~(3, 5)、(7, 5)~(9, 5) 候选数中 的数字 7、8 都安全的删减掉;于是(8, 5)的候选数 3、7、8 将再度被删减成 3;出现了唯一候选数啦! 像<图 1>~<图 3>这样,只做一次区块删减就找到下一个解的情况固然是不错,但有时并没有那么顺心, 像<图 4>就需要删减三次才得到下一个解,不过那还算好的了,因为三次的删减都恰好发生在同一个区块中, 请看下面发生在不同区块的情形吧! 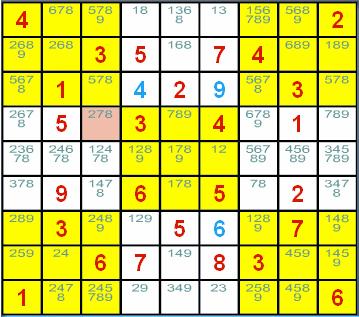 <图 5> <图 5> 中的(4, 3)将可利用区块删减法得出下一个解,你能够不看下面的解答,自己找出来吗?试试! 也许你已经找出答案了,恭喜!也许你还找不出答案,那也没关系,人有失手,马有失蹄,总有脑袋被浆糊 糊住而一时失误的时候,请看答案吧:因为第 8 列的数字 2 只出现在 (8, 1)~(8, 3) 这一个区块, 所以可以将下左九宫格的另两个区块 (7, 1)~(7, 3)、(9, 1)~(9, 3) 候选数中的数字 2 安全的删减掉; 删减之后的结果如<图 6>。 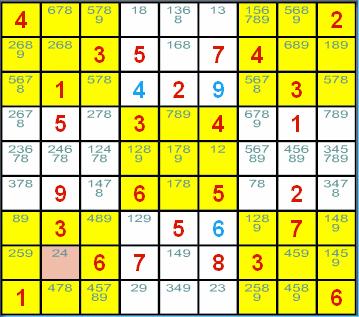 <图 6> 接下来,因为第 3 行的数字 2 只出现在 (4, 3)~(6, 3) 这一个区块,所以可以将中左九宫格的另两个区块 (4, 1)~(6, 1)、(4, 2)~(6, 2) 候选数中的数字 2 安全的删减掉;删减之后的结果如<图 7>。 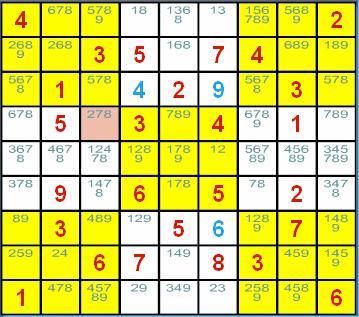 <图 7> 哈!哈!看出来了吗?(4, 3)已出现了列隐性唯一候选数 2 啦! (责任编辑:admin) |