复数的萌芽、形成与发展
http://www.newdu.com 2025/12/11 04:12:28 人民教育出版社 佚名 参加讨论
复数的萌芽、形成与发展 山东胜利油田第一中学 张洪杰 我们知道,在实数范围内,解方程 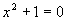 是无能为力的,只有把实数集扩充到复数集才能解决。对于复数a+bi(a、b都是实数)来说,当b=0时,就是实数;当b≠0时叫虚数,当a=0,b≠0时,叫做纯虚数。可是,历史上引进虚数,把实数集扩充到复数集可不是件容易的事,那么,历史上是如何引进虚数的呢? 是无能为力的,只有把实数集扩充到复数集才能解决。对于复数a+bi(a、b都是实数)来说,当b=0时,就是实数;当b≠0时叫虚数,当a=0,b≠0时,叫做纯虚数。可是,历史上引进虚数,把实数集扩充到复数集可不是件容易的事,那么,历史上是如何引进虚数的呢?16世纪意大利米兰学者卡当(1501—1576)在1545年发表的《重要的艺术》一书中,公布了三次方程的一般解法,被后人称之为“卡当公式”。他是第一个把负数的平方根写到公式中的数学家,并且在讨论是否可能把10分成两部分,使它们的乘积等于40时,他把答案写成 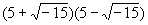 =40,尽管他认为 =40,尽管他认为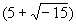 和 和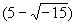 这两个表示式是没有意义的、想象的、虚无飘渺的,但他还是把10分成了两部分,并使它们的乘积等于40。给出“虚数”这一名称的是法国数学家笛卡尔(1596—1650),他在《几何学》(1637年发表)中使“虚的数’‘与“实的数”相对应,从此,虚数才流传开来。 这两个表示式是没有意义的、想象的、虚无飘渺的,但他还是把10分成了两部分,并使它们的乘积等于40。给出“虚数”这一名称的是法国数学家笛卡尔(1596—1650),他在《几何学》(1637年发表)中使“虚的数’‘与“实的数”相对应,从此,虚数才流传开来。数系中发现一颗新星──虚数,于是引起了数学界的一片困惑,很多大数学家都不承认虚数。德国数学家菜不尼茨(1664—1716)在1702年说:“虚数是神灵遁迹的精微而奇异的隐避所,它大概是存在和虚妄两界中的两栖物”。瑞士数学大师欧拉(1707—1783)说;“一切形如 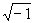 , ,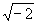 习的数学武子都是不可能有的,想象的数,因为它们所表示的是负数的平方根。对于这类数,我们只能断言,它们既不是什么都不是,也不比什么都不是多些什么,更不比什么都不是少些什么,它们纯属虚幻。”然而,真理性的东西一定可以经得住时间和空间的考验,最终占有自己的一席之地。法国数学家达兰贝尔(1717—1783)在1747年指出,如果按照多项式的四则运算规则对虚数进行运算,那么它的结果总是 习的数学武子都是不可能有的,想象的数,因为它们所表示的是负数的平方根。对于这类数,我们只能断言,它们既不是什么都不是,也不比什么都不是多些什么,更不比什么都不是少些什么,它们纯属虚幻。”然而,真理性的东西一定可以经得住时间和空间的考验,最终占有自己的一席之地。法国数学家达兰贝尔(1717—1783)在1747年指出,如果按照多项式的四则运算规则对虚数进行运算,那么它的结果总是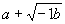 的形式(a、b都是实数)(说明:现行教科书中没有使用记号 的形式(a、b都是实数)(说明:现行教科书中没有使用记号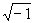 =-i,而使用 =-i,而使用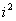 =一1)。法国数学家棣莫佛(1667—1754)在1730年发现公式了 =一1)。法国数学家棣莫佛(1667—1754)在1730年发现公式了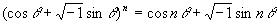 ,这就是著名的探莫佛定理。欧拉在1748年发现了有名的关系式 ,这就是著名的探莫佛定理。欧拉在1748年发现了有名的关系式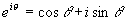 ,并且是他在《微分公式》(1777年)一文中第一次用i来表示一1的平方根,首创了用符号i作为虚数的单位。“虚数”实际上不是想象出来的,而它是确实存在的。挪威的测量学家成塞尔(1745—1818)在1779年试图给于这种虚数以直观的几何解释,并首先发表其作法,然而没有得到学术界的重视。 ,并且是他在《微分公式》(1777年)一文中第一次用i来表示一1的平方根,首创了用符号i作为虚数的单位。“虚数”实际上不是想象出来的,而它是确实存在的。挪威的测量学家成塞尔(1745—1818)在1779年试图给于这种虚数以直观的几何解释,并首先发表其作法,然而没有得到学术界的重视。德国数学家高斯(1777—1855)在1806年公布了虚数的图象表示法,即所有实数能用一条数轴表示,同样,虚数也能用一个平面上的点来表示。在直角坐标系中,横轴上取对应实数a的点A,纵轴上取对应实数b的点B,并过这两点引平行于坐标轴的直线,它们的交点C就表示复数a+bi。象这样,由各点都对应复数的平面叫做“复平面”,后来又称“高斯平面”。高斯在1831年,用实数组(a,b)代表复数a+bi,并建立了复数的某些运算,使得复数的某些运算也象实数一样地“代数化”。他又在1832年第一次提出了“复数”这个名词,还将表示平面上同一点的两种不同方法──直角坐标法和极坐标法加以综合。统一于表示同一复数的代数式和三角式两种形式中,并把数轴上的点与实数—一对应,扩展为平面上的点与复数—一对应。高斯不仅把复数看作平面上的点,而且还看作是一种向量,并利用复数与向量之间—一对应的关系,阐述了复数的几何加法与乘法。至此,复数理论才比 较完整和系统地建立起来了。 经过许多数学家长期不懈的努力,深刻探讨并发展了复数理论,才使得在数学领域游荡了200年的幽灵──虚数揭去了神秘的面纱,显现出它的本来面目,原来虚数不虚呵。虚数成为了数系大家庭中一员,从而实数集才扩充到了复数集。 随着科学和技术的进步,复数理论已越来越显出它的重要性,它不但对于数学本身的发展有着极其重要的意义,而且为证明机翼上升力的基本定理起到了重要作用,并在解决堤坝渗水的问题中显示了它的威力,也为建立巨大水电站提供了重要的理论依据。 多考资料; 《趣味数学史话》张开新 选自《中学生数学》2001年4月上 (责任编辑:admin) |