需要多少保安
http://www.newdu.com 2025/12/12 03:12:05 人民教育出版社 佚名 参加讨论
需要多少保安 Panot公司的董事会正在召开每月一度的例会。当会议主席宣布讨论议程中的最后一项——Warthog美术收藏品——时,董事长Boss Parrot满意地点了点头。这些美术收藏品将要陈列在一个高技术的美术馆中(Parrot喜欢将它称为“现代化的”美术馆),该馆用来展出无与伦比的艺术家Sandy Warthog的全部作品。Parrot是Warthog的花哨而怪异的作品风格的早期崇拜者之一,他拥有Warthog创作出的每一幅画。 “安全问题是非常重要的”,财务部门的负责人指出。 “当然,Warthog美术收藏品将配备一切最新的电子监视设备”,保卫部门的头头Harry Sams说,“每幅画都将有一台单独的微型摄像机对着——” “不,我希望对Warthog美术收藏品采取点特殊的安全手段”,Paorrot打断了他的话。 “晤——要多特殊呢?” “真正地特殊,Harry。我希望用看守。就是保安人员。” “嘿,老板,我看我们还是不要要求太高了吧?你知道单是安全审查就得花多少钱吗?更不用说还有医疗保险、解聘费、咖啡费等等开支了。用活人就得多花钱,老板。这样不行。我建议是采用Notsobitchi公司生产的最新式嗅探机器人,或许还有一些——” “我希望用保安人员,Harry。” “是,老板。保安人员。晤——要多少呢?” “保安人员的人数,要足以保证美术馆的每一平方英寸都至少在一名保安人员的监视之下。我希望每个保安人员都坐在一张旋转坐椅上,这样他们就有全方位的视界。聘请的保安人员的人数应满足保卫工作的需要——但多一个也不行,懂吗?你知道,活人就得多花 钱。 “是的,老板先生。晤——美术馆的平面图已定稿了吧”? “还没有。” “既然这样,那就不好确定需要多少保安人员了。” “建筑师已经决定,美术馆只有一层,且有24面笔直的墙——每一面墙代表Warthog的某一时期的作品风格。我的任务是:既然你手头没有完备的资料,我授权你聘用一定数量的保安人员,其人数要不多不少,刚好足以保证任何一个有24面直墙的房间处于保安人员的监视之下,每个保安人员的位置固定,且其视界为全方位的。但我希望你聘请的人数不要超过你的实际需要。如果事实证明Warthog美术收藏品需要的保安人员人数少于理论极大值,我将承担责任,但如果美术馆的任何一种设计方案都不需要你聘请的那么多保安人员,或者你聘请的保安人员不敷需要,那么你只得另找老板了,Harry。” 如果你是一位权力很大的经理;而你的饭碗又面临被打碎的危险,你自然不会安然自得地混日子了。你会花公司的很大一笔钱去聘请用这笔钱能够请到的最好的咨询专家,并要他们来解决这个问题。 Harry从电话簿上找到了这些专家:一个称为“月光数学家”的团体。专家名为Alf Moon和Dee Light。 “这是个棘手的问题,Sams先生”,Moon说。 “的确棘手”,Light说道。他已经知道答案。但是告诉客户这类事情是不会赚到钱的。 “问题在于”,Moon继续说下去,“排布24条直线的方法多得数不胜数。”这两位专家有轮流发言的习惯。 “而你需要的保安人员的数目又与你采用何种布置方式有关。” “幸运的是,我们有一些好方法可用。这些方法属于我们这行所谓的‘美术馆定理’。” “是的,完全正确。比如说,如果一个房间只需一名保安人员,那它必定是我们称之为星形的房间。” “这就意味着存在着某个内点或边界点,使得房间中的任何一点均可用一条完全在房间内的直线与该点连接起来。” “现在,想象你用任何一种老办法把一定数量的保安人员布置在一个房间内。这样每个保安人员都守在一个星形区域中——也就是他或她能够监视到的那部分房间。而你问的问题就是——” “任何一个有24面墙壁的房间所能分解成的星形区域最少有多少个”,Moon说道,同时很快地在他的笔记本上画出了草图。 “不见得吧”,Harry说。 “那么在这个具体的房间中,采用这种具体的保安人员布置方案”,Moon继续说道,“你可以看出我已经画出来的三个保安人员能够监视除了6个孤立区域之外的整个房间。” “而这6个区域是凸的”,Light指出。 “特别是,这就意味着这些区域是星形区域。” “因此,如果你在每个这类区域中再布置一名保安人员,使保安人员的总数达到9人,那么整个房间全都在保安人员监视之下了。” “好极了!”Harry说,“这么说来我需要9名保安人员了?” Moon和Light狡猾地摇摇头。“完全不是的,Sams先生。首先,这是因为对这个具体的房间采说可能有某种只需要较少保安人员的方案就完全够用了——” “其次,这也是因为其他某种房间可能需要更多的保安人员。” “我来总结一下”,Sams说,“答案或者是9,或者比9少,或者比9多。” “你明白啦。” “本公司给你们的报酬是多少?” “你正好体验到这个问题啦,Sams先生”,Moon说,“很明显,对这个问题我们得采用一种有条理的方法。” “‘如有有疑问的话,就把它分解’”,Light说。“我们需要把房间分解成许多较小的部分,然后尝试通过尽可能有效的方式把它们重新组合成星形区域。” “是的。你认为该怎么做才好呢,Light?” “‘要使问题简化,就把它划分成三角形。’我认为三角形是用起来最自然的图形,Moon,你同意吗?” “是的。但把一个房间分成三角形的方法可不少。” “当然。我建议我们在把房间划分为三角形时不要引入新的顶点。”她转向Sams。“顶点(Vertex)是我们这行的一个术语,指的是 房间角落处的点。”Sams点点头。 “你的意思是说仅仅使用房间本身已经有的哪些顶点吗?”Moon问道。“你是否总能做到这一点呢?” “绝无问题。如果你希望的话,我可以证明给你看。” “不用了,继续说下去吧。这问题开始有点令人感兴趣了。” “接着我将把房间的每个顶点着上颜色。我只使用三种颜色——比如说红、黄和蓝——这样每个三角形恰好有一个顶点涂上三种颜色中的一种。任选一个三角形对其着色,使它的每个顶点各涂上一种不同颜色,然后再向外扩展。每个相邻的三角形上的颜色都是被完全决定了的,因为这些相邻三角形都只剩下一个顶点未被着色,因此你只需用与另外两个顶点不同的颜色来给它着色就行了。这样有条不紊地进行下去,最后就可把所有顶点都涂上颜色了。” “不错。现在看看我们把上述方法用在你的图形上时会出现什么情况。你最终得到6个红色顶点,9个蓝色顶点和9个黄色顶点。如果你在每个红色顶点上安排一个保安人员,那么他们就能看到整个房间。由于每个保安人员均能监视以他或她为其顶点之一的每个三角形——” “而且每个三角形都有一个红色顶点。毫无疑问。这真是干净利落。这个房间仅需要6位保安人员,而不是我们开始时确定的9位。我们把这些研究人员安排在角落上。” “是安排在顶点上。”Light向前倾了倾身子,脸上带着一种古怪的表情。“现在,Moon,我的朋友,我希望你看出如何推广这一论据?” Moon在房间里走来走去,激动地挥舞着手臂。“是的,是的。如果一个房间有24面墙,那么它就有24个角落。如果我们把房间分解成三角形,并按照你的原则对其着色,那么我们就选择出现次数最少的那种颜色,并将保安人员安置在这种颜色对应的顶点上。” “的确如此。既然红色、蓝色和黄色顶点的总数为24,那么无论这些颜色是如何分配的,至少有一种颜色出现的次数不能超过8次。” “你的意思是说,如果三个数加起来等于24,那么它们不可能同时为9或大于9?是的,我明白了。” Light咧嘴笑了一下。“这样我就证明了任何有24面墙的房间可用最多8名保安人员来保卫。” “且慢”,Sams说道,他一直在注意听着两人的对话。“你刚才说这个特定的房间只需6名保安人员,而不是8名。” 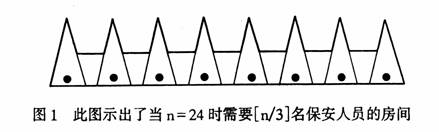 “不错,Sams先生。但为了保证任何一个有24面墙的房间的安全,我们还得求出最少必须要多少名保安人员。我们刚才证明的就是至多8名保安人员就够了。” “因此,我们所要做的事情就是找出一个有24面墙且需要8名保安人员的房间”,Light说。 “这很容易”,Moon说,“这个房间就能解决问题。”他很快画了个草图(见图2)。“保安人员必须安排得使他们能监视到8个三角形凹室,这样就产生了8个互不重叠的区域,因此每个区域必须各有一名保安人员。另外,我对保安人员的安排方式表明有8名保安人员就足以应付了。” “你没有把保安人员安置在角落上,”Harry提出异议。 “我们可以把保安人员安排在角落上,而且对一般性的证明来说,这样安排是有好处的”,Moon耐心地解释道,“但我们不一定非得这样安排不可。在上面所举的例子中,不这样安排还更简单一些。 “好吧”,Smas说,“8名保安人员。好极了。我将告诉Boss Parrot说问题已经解决——”他话还没说完,电话铃响起来了。 Sams抓起电话。他点了几次头,咕哝着说了些什么,然后把电话小心地放回桌上。接着他抓起一个花瓶猛掷到房间的另一边,在花瓶的碎片上跳上跳下,嘴里不连贯地吼叫着。  “遇到麻烦了吗,Sams先生?”Light问道,自认为她的问题很得体。 “那个该死的笨蛋建筑师改变了设计规范”,Sams大叫着。“现在美术馆将有173面墙,以便绘画作品不但能按代表一定风格的时期,而且也能按主题内容安排。” “没有问题的,Sams先生。由于我们发现的是一般性的方法,它仍然适用的。如果你根据Light的规则把房间的各个顶点涂上颜色,那么就只需把保安人员安排在出现次数最少的颜色所在的那些顶点上。现在既然3个数之和为173,那么其中某个数必定至多为173/3=572/30” “你是说我需要572/3名保安人员?老板会不高兴的。” “不。这只意味着某种颜色最多出现57次,因此你聘请57名保安人员就行了。画一个同我刚才画的那幅图(见图2)相似的图形,就可证明一般说来少于57名保安人员是不够的。” Light说:“我们已经证明了的就是有几个顶点的房间最多需要[n/3]名保安人员,这里方括号表示‘取整数部分’。这一答案是捷克数学家Vaclav Chvatal于1973年发现的。我给出的证明则是鲍登学院的S·FisK l978年发现的简化证明,此外——” 电话铃又响了起来。Sams接了电话。“你们会相信吗?折腾了半天之后,建筑设计师又要用24面墙的方案了,说是关于Warthong作品主题的问题争论太多了。很好,请你们给公司开个帐单,并在星期四之前交给我一份附有实施要点的完整报告。我和Boss Parrot有一个约会。” “我们非常仰幕Boss Parrot”,Moon说。 “我们也能来见见Parrot先生吗?”Light请求道。“我们希望会见这位了不起的人。大概永远不会再有这种机会了。” Sams想了一会,最后答应了。无论如何,带他们一起去给自己打气壮胆不会有什么害处的。万一有什么技术性问题冒出来呢。 “你是说要8名保安人员?干得不错,Sams。”Parrot高兴地微笑着。“正好建筑师刚刚定下了美术馆的最终布局方案。你来指给我看看这些保安人员该布置在什么地方。”他把美术馆平面图铺开在桌子上。 Sams向平面图看了一眼,不由得怔住了。随后他似乎恍然大悟,绝望地盯着Moon和Light。Moon用肘轻轻地推了Light一下,悄悄地:“呵!有洞。没有任何人讲过关于洞的情况。对这种房间8名保安人员是不够的。我只凭一看就可以肯定。” “不。嗯——,有一个猜想是说如果有h个洞和n面墙——” “包括洞上的墙在内吗?” “嗯?当然包括——那么所需的保安人员最多为[(n十h)/3]名。这平面图的n=24,而h=3,所以9名保安人员就应该——” “你们两位在悄悄说些什么呀?”Parrot狐疑地插了进来。 “请原谅,先生。我们在赞赏建筑师的设计方案。”Light丢给Sams一个暗示的眼色,然后从口袋里掏出一支笔。“好了,正如Sams先生所说,当房间有24面墙时,8名保安人员在任何情况下都足够了。当然,不用说还得加上一名主管人——总得有个人负责把他们的工作安排妥当。是这样吧。 Sams先生?” 额头上渗满汗珠的Sams这才恢复了镇定。“是的,Light小姐,当然我也想要有一名主管人。” “这样你们总共需要9名保安人员,先生,正如Sams先生刚才告诉的那样。” “这些都将记载在实施要点上,老板”,Sams说。他又逐渐变得泰然自若起来。 他斜看了Moon和Light一眼,而后者则让人几乎觉察不到的方式向他点了点头。9名保安人员?这不是他们一开始时提出的数字吗?不管怎样,现在的问题是如何安排这些保安人员的位置了。当然这些月光数学家们是知道的。 不知怎么的Sams觉得他们刚刚提高了他们的等级。 (责任编辑:admin) |
- 上一篇:来自大海的数学宝藏
- 下一篇:哪种投票制度最合理?