龟背上的学问
http://www.newdu.com 2025/12/09 03:12:36 人民教育出版社 佚名 参加讨论
龟背上的学问 传说大禹治水时,在一次疏通河道中,挖出了一只大龟,人们很是惊讶,争相观看,只见龟背上清晰刻着图1所示的一个数字方阵。  这个方阵,按《孙子算经》中筹算记数的纵横相间制:“凡算之法,先识其位。一纵十横,百立千僵,千十相望,万百相当。六不积算,五不单张。”可译成现代的数字,如图2所示。 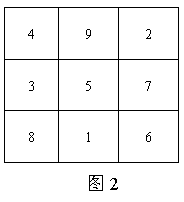 方阵包括了九个数字,每一行一与列的数字和均为15,两条对角线上的数也有相同的性质。当时,人们以为是天神相助,治水有望了。后来,人们称刻在龟背上的方阵为“幻方”(国外称为“拉丁方”),属于组合数学范畴。使用整数1—9构成的3×3阶“拉丁方”唯一可能的和数是15,这一点只要把这“拉丁方”中所有数加起来便可证明,1十2十3十4十5十6十7十8十9=45,要把这几个数分配到三行(或列)使得每行(或列)有同样的和,那么,每行(或列)的和应为45/3=150 组合数学是数学中的一个分支,在实际生活中应用很广泛,请看下面的例子。 5名待业青年,有7项可供他们挑选的工作,他们是否能找到自己合适的工作呢?由于每个人的文化水平、兴趣爱好及性别等原因,每个人只能从七项工作中挑选某些工种,也就是说每个人都有一张志愿表,最后根据需求和志愿找到一个合适的工作。 组合数学把每一种分配方案叫一种安排。当然第一个问题是考虑安排的存在性,这就是存在问题;第二个问题是有多少种安排方法,这就是计数问题。接下去要考虑在众多的安排中选择一种最好的方案,这就是所谓的“最优化问题”。 存在问题、构造问题、计数问题和最优化问题就构成了全部组合数学的内容。如果你想了解更多的组合数学问题,那就要博览有关书籍,你会得到许多非常有趣的知识,会给你许多的启发和教益。 (责任编辑:admin) |