e和银行业
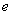 跟我们日常的事情有什么关系呢?事实上它在我们日常生活中,跟任何一个特定的整数一样,尽管人们并不总能察觉到它的出现。只有人知道 跟我们日常的事情有什么关系呢?事实上它在我们日常生活中,跟任何一个特定的整数一样,尽管人们并不总能察觉到它的出现。只有人知道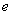 是一个实际的数,如果问大家,可能多数人会说 是一个实际的数,如果问大家,可能多数人会说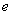 是英语字母表里的第5个字母。大家知道它是一个奇怪的数,这是我们通过数学课了解到的。只有少数人知道它是一个无理数和一个超越数。 是英语字母表里的第5个字母。大家知道它是一个奇怪的数,这是我们通过数学课了解到的。只有少数人知道它是一个无理数和一个超越数。

在今天的银行业里,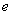 是对银行家最有帮助的一个数。人们可能会问,像 是对银行家最有帮助的一个数。人们可能会问,像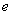 这样的数是怎样又以何种方式与银行业发生关系呢?要知道后者是专门跟“元”和“分”打交道的! 这样的数是怎样又以何种方式与银行业发生关系呢?要知道后者是专门跟“元”和“分”打交道的!
假如没有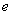 的发现,银行家要计算今天的利息就要花费极其大量的时间,无论是逐日逐日地算复利,还是持续地算复利都无法避免。有幸的是, 的发现,银行家要计算今天的利息就要花费极其大量的时间,无论是逐日逐日地算复利,还是持续地算复利都无法避免。有幸的是,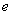 的出现助了一臂之力。 的出现助了一臂之力。
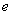 的定义是作为数列 的定义是作为数列 的极限。我们通常写为 的极限。我们通常写为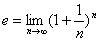 。在利息计算中怎样借助于这个公式呢?实际的计算公式是:本利和 。在利息计算中怎样借助于这个公式呢?实际的计算公式是:本利和 , , 。 。
这里 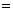 本金, 本金, 年利率, 年利率,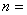 一年之内计算利息的次数, 一年之内计算利息的次数,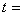 存钱的年数。 存钱的年数。
上述公式可以变形为对于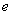 的公式。当人们投资1美元年利率为100%时,一年的本利和可达 的公式。当人们投资1美元年利率为100%时,一年的本利和可达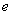 美元。开头可能会有人以为总计会是一个天文数字,但看了下面的估计后就会知道它接近于 美元。开头可能会有人以为总计会是一个天文数字,但看了下面的估计后就会知道它接近于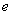 的值。 的值。

于是,我们看到:如果我们投资1美元,年利率为100%,那么收益决不会超过2.72美元。事实上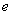 的小数点后头22位数是 的小数点后头22位数是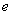 =2.7182818284590452353602。 =2.7182818284590452353602。
下一个问题是怎样对 进行工作。最好先通过尝试来确定看。比如说我们从1000美元开始以年利8%存入银行,让我们看看当按一年期计算,然后按每半年期计算,再按每三个月期计算复利时会出现什么。 进行工作。最好先通过尝试来确定看。比如说我们从1000美元开始以年利8%存入银行,让我们看看当按一年期计算,然后按每半年期计算,再按每三个月期计算复利时会出现什么。

如果逐日计算复利,可用公式 。这个公式如果用手算则要花好多时间,但今天用电子计算器和专门的计算机顷刻间便能得出结果。 。这个公式如果用手算则要花好多时间,但今天用电子计算器和专门的计算机顷刻间便能得出结果。
(责任编辑:admin)
|





