整数的性质及其应用(1)
http://www.newdu.com 2025/09/22 01:09:17 人民教育出版社 佚名 参加讨论
整数的性质及其应用(1) 基础知识 整数的性质有很多,这里我们着重讨论整数的整除性、整数的奇偶性,质数与合数、完全平方数及整数的尾数等几个方面的应用。 1.整除的概念及其性质 在高中数学竞赛中如果不加特殊说明,我们所涉及的数都是整数,所采用的字母也表示整数。 定义:设 由整除的定义,容易推出以下性质: (1)若 (2)若 (3)若 (4) (5) (6)(带余除法)设 易知,带余除法中的商实际上为 若 若 (7)如果在等式 (8)n个连续整数中,有且只有一个是n的倍数; (9)任何n个连续的整数之积一定是n!的倍数,特别地,三个连续的正整数之积能被6整除; 2.奇数、偶数有如下性质: (1)奇数 (2)奇数的平方都可以表示成 (3)任何一个正整数 (4)若有限个整数之积为奇数,则其中每个整数都是奇数;若有限个整数之积为偶数,则这些整数中至少有一个是偶数;两个整数的和与差具有相同的奇偶性;偶数的平方根若是整数,它必为偶数。 3.完全平方数及其性质 能表示为某整数的平方的数称为完全平方数,简称平方数。平方数有以下性质与结论: (1)平方数的个位数字只可能是0,1,4,5,6,9; (2)偶数的平方数是4的倍数,奇数的平方数被8除余1,即任何平方数被4除的余数只有可能是0或1; (3)奇数平方的十位数字是偶数; (4)十位数字是奇数的平方数的个位数一定是6; (5)不能被3整除的数的平方被3除余1,能被3整数的数的平方能被3整除。因而,平方数被9也合乎的余数为0,1,4,7,且此平方数的各位数字的和被9除的余数也只能是0,1,4,7; (6)平方数的约数的个数为奇数; (7)任何四个连续整数的乘积加1,必定是一个平方数。 (8)设正整数 4.整数的尾数及其性质 整数 (1) (3) (5)若 (7) (8)  5.整数整除性的一些数码特征(即常见结论) (1)若一个整数的未位数字能被2(或5)整除,则这个数能被2(或5)整除,否则不能; (2)一个整数的数码之和能被3(或9)整除,则这个数能被3(或9)整除,否则不能; (3)若一个整数的未两位数字能被4(或25)整除,则这个数能被4(或25)整除,否则不能; (4)若一个整数的未三位数字能被8(或125)整除,则这个数能被8(或125)整除,否则不能; (5)若一个整数的奇位上的数码之和与偶位上的数码之和的差是11的倍数,则这个数能被11整除,否则不能。 6.质数与合数及其性质 1.正整数分为三类:(1)单位数1;(2)质数(素数):一个大于1的正整数,如果它的因数只有1和它本身,则称为质(素)数;(3)如果一个自然数包含有大于1而小于其本身的因子,则称这个自然数为合数。 2.有关质(素)数的一些性质 (1)若 (2)若 (3)设 (4)(算术基本定理)任何一个大于1的正整数 (5)任何大于1的整数 (6)若 典例分析 例1.证明: 证明: 所以 例2.对正整数 证明:设 对于 例3.设 证明: 由k是正奇数,从而结于每一个 例4.设 证明:首先,当 最后, 例5.设正整数 证法一:由 同理,存在正整数 因此, 注:若正整数 证法二:由 若它是一个素数,设为 可见 例6.求出有序整数对( 解:由于 又 若 然而 例7.证明:若正整数 证法一:已知关系式即为 若 不妨设 从而 因为 而②式又可写成 因为 所以 所以 所以 证法二:已知关系式即为 论证的关键是证明正整数 记 例8.证明不存在正整数 证明:假设存在这样的正整数 (2n2+1)(3n2+1)(6n2+1)也必定是完全平方数。 而(2n2+1)(3n2+1)(6n2+1)=36n6+36n4+11n2+1; 所以 例9.数列 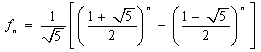 , ,记 解:记 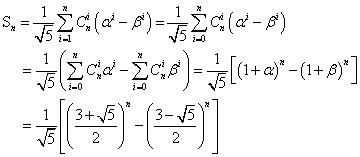 注意到 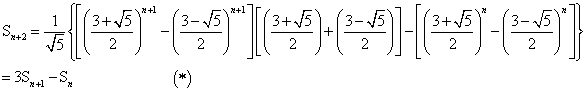 因此,Sn+2除以8的余数,完全由Sn+1、Sn除以8的余数确定 故当且仅当 练习题 1.证明:如果 证明:因为 2.设 解:由 又因为 3.证明:对于任意正整数 因为若 若 故 所以 4.已知 证明:因为若 若 所以 又 5.设a、b、c为满足不等式1<a<b<c的整数,且(ab-1)(bc-1)(ca-1)能被abc整除,求所有可能数组(a,b,c).(1989年上海竞赛试题) 解 ∵(ab-1)(bc-1)(ca-1) =a2b2c2-abc(a+b+c)+ab+ac+bc-1,① ∵abc|(ab-1)(bc-1)(ca-1). ∴存在正整数k,使ab+ac+bc-1=kabc, ② k= 若a≥3,此时1= 已知a>1. ∴只有a=2. 当a=2时,代入②中得2b+2c-1=bc,即 1= ∴0<b<4,知b=3,从而易得c=5. 说明:在此例中通过对因数k的范围讨论,从而逐步确定a、b、c是一项重要解题技巧. (责任编辑:admin) |
- 上一篇:高中数学竞赛讲义(十七)
- 下一篇:高中数学竞赛讲义(八)