《1.1.3 集合的基本运算》测试题
一、选择题
1.若全集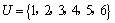 , , , ,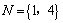 ,则集合 ,则集合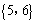 等于( ). 等于( ).
A. B. B. C. C. D. D.
考查目的:考查集合的基本运算.
答案:D.
解析:由题意知 , , , , , , ,故本题应选D. ,故本题应选D.
2.设全集U是实数集R, , , ,则图中阴影部分所表示的集合是( ). ,则图中阴影部分所表示的集合是( ).

A.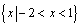 B. B.
C. D. D.
考查目的:考查文氏图的识读、表示以及集合的基本运算.
答案:C.
解析:由图知,阴影部分表示的集合为 ,再根据集合的运算知,本题答案选C. ,再根据集合的运算知,本题答案选C.
3.设集合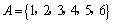 , , ,则满足 ,则满足 ,且 ,且 的集合 的集合 的个数为( ). 的个数为( ).
A.56 B.49 C.57 D.8
考查目的:考查集合间的基本关系、集合的基本运算以及子集问题.
答案:A
解析:集合A的所有子集共有 个,其中不含4,5,6,7的子集有 个,其中不含4,5,6,7的子集有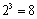 个,所以集合 个,所以集合 共有56个,故本题选A. 共有56个,故本题选A.
二、填空题
4.设集合 , , , , ,则 ,则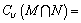 . .
考查目的:考查集合的交并补的计算方法.
答案:
解析:由题知 ,进而求出其补集为 ,进而求出其补集为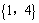 . .
5.已知集合 ,则 ,则 . .
考查目的:考查两个集合代表元素的辨认与交集的运算.
答案: . .
解析:由于A是点集,B是数集,∴ . .
6.设 ,且 ,且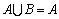 ,则实数 ,则实数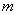 的取值范围是 . 的取值范围是 .
考查目的:考查集合运算及集合间的关系.
答案: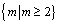
解析:∵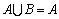 ,∴ ,∴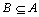 ,∴ ,∴ . .
三、解答题
7.若集合 , , ,且 ,且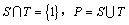 ,求集合P的所有子集. ,求集合P的所有子集.
考查目的:考查集合运算及集合间的关系.
答案: . .
解析:由 ,且 ,且 得 得 ,则 ,则 ,且 ,且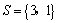 . .
当 时, 时, ,即 ,即 ,满足 ,满足 ; ;
当 时, 时, ,即 ,即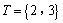 ,不满足 ,不满足 ; ;
∴ , ,
那么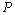 的子集有 的子集有 . .
8.设 ,若 ,若 ,求 ,求 的值. 的值.
考查目的:考查集合运算及集合间的关系.
答案: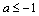 ,或 ,或 . .
解析:∵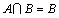 ,∴ ,∴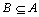 . .
∵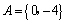 ,∴ ,∴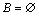 ,或 ,或 ,或 ,或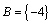 ,或 ,或 . .
当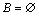 时,方程 时,方程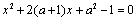 无实数根,则 无实数根,则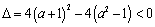 ,整理得 ,整理得  ,解得 ,解得  . .
当 时,方程 时,方程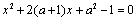 有两等根均为0,则 有两等根均为0,则 ,解得 ,解得 . .
当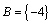 时,方程 时,方程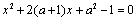 有两等根均为-4,则 有两等根均为-4,则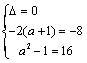 ,无解; ,无解;
当 时,方程 时,方程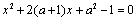 的两根分别为0,-4,则 的两根分别为0,-4,则 ,解得 ,解得 . .
综上所述,得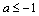 ,或 ,或 . .
(责任编辑:admin)
|

 ,解得
,解得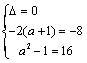 ,无解;
,无解; ,解得
,解得