2018高考数学二轮复习直线的方程知识专题总结
http://www.newdu.com 2025/11/09 08:11:10 三好网 佚名 参加讨论
2018年高考二轮复习是高考成绩提升的关键期,考生一定要积极备考,梳理高中学科知识脉络,牢记知识点。小编整理了2018高考数学二轮复习知识点,直线的方程知识总结如下:  一、直线与方程 (1)直线的倾斜角 定义:x轴正向与直线向上方向之间所成的角叫直线的倾斜角。特别地,当直线与x轴平行或重合时,我们规定它的倾斜角为0度。因此,倾斜角的取值范围是0180 (2)直线的斜率 ①定义:倾斜角不是90的直线,它的倾斜角的正切叫做这条直线的斜率。直线的斜率常用k表示。即。斜率反映直线与轴的倾斜程度。当时,。当时,;当时,不存在。 ②过两点的直线的斜率公式: 注意下面四点:(1)当时,公式右边无意义,直线的斜率不存在,倾斜角为90 (2)k与P1、P2的顺序无关; (3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得; (4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。 (3)直线方程 ①点斜式:直线斜率k,且过点 注意:当直线的斜率为0时,k=0,直线的方程是y=y1。当直线的斜率为90时,直线的斜率不存在,它的方程不能用点斜式表示.但因l上每一点的横坐标都等于x1,所以它的方程是x=x1。 ②斜截式:,直线斜率为k,直线在y轴上的截距为b ③两点式:()直线两点, ④截矩式:其中直线与轴交于点,与轴交于点,即与轴、轴的截距分别为。 ⑤一般式:(A,B不全为0) ⑤一般式:(A,B不全为0) 注意: 1.各式的适用范围 2.特殊的方程如:平行于x轴的直线:(b为常数);平行于y轴的直线:(a为常数); (4)直线系方程:即具有某一共同性质的直线 (一)平行直线系 平行于已知直线(是不全为0的常数)的直线系:(C为常数) (二)过定点的直线系 (ⅰ)斜率为k的直线系:,直线过定点; (ⅱ)过两条直线,的交点的直线系方程为(为参数),其中直线不在直线系中。 (5)两直线平行与垂直 当,时,;注意:利用斜率判断直线的平行与垂直时,要注意斜率的存在与否。 (6)两条直线的交点 相交:交点坐标即方程组的一组解。方程组无解;方程组有无数解与重合 (7)两点间距离公式:设是平面直角坐标系中的两个点,则 (8)点到直线距离公式:一点到直线的距离 (9)两平行直线距离公式:在任一直线上任取一点,再转化为点到直线的距离进行求解。 高中数学知识点一:直线方程的一般式关于x和y的一次方程都表示一条直线.我们把方程写为Ax+By+C=0,这个方程(其中A、B不全为零)叫做直线方程的一般式. 高中数学知识点二:直线方程的不同形式间的关系直线方程的五种形式的比较如下表: 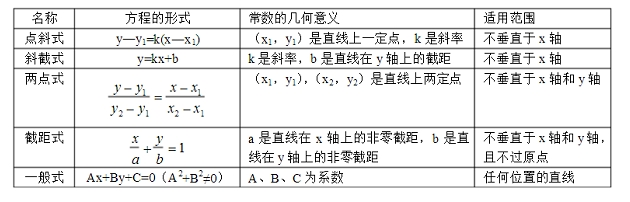 高中数学知识点三:直线方程的综合应用 1.已知所求曲线是直线时,用待定系数法求. 2.根据题目所给条件,选择适当的直线方程的形式,求出直线方程.对于两直线的平行与垂直,直线方程的形式不同,考虑的方向也不同. 高中数学直线方程知识点:表达方式 高中数学知识点1:一般式:Ax+By+C=0(A、B不同时为0)【适用于所有直线】 高中数学知识点2:点斜式:y-y0=k(x-x0) 【适用于不垂直于x轴的直线】 表示斜率为k,且过(x0,y0)的直线 高中数学知识点3:截距式:x/a+y/b=1【适用于不过原点或不垂直于x轴、y轴的直线】 表示与x轴、y轴相交,且x轴截距为a,y轴截距为b的直线 高中数学知识点4:斜截式:y=kx+b【适用于不垂直于x轴的直线】 表示斜率为k且y轴截距为b的直线 高中数学知识点5:两点式:【适用于不垂直于x轴、y轴的直线】 表示过(x1,y1)和(x2,y2)的直线 (y-y1)/(y2-y1)=(x-x1)/(x2-x1) (x1≠x2,y1≠y2) 高中数学知识点6:交点式:f1(x,y) *m+f2(x,y)=0 【适用于任何直线】 表示过直线f1(x,y)=0与直线f2(x,y)=0的交点的直线 高中数学知识点7:点平式:f(x,y) -f(x0,y0)=0【适用于任何直线】 表示过点(x0,y0)且与直线f(x,y)=0平行的直线 高中数学知识点8:法线式:x·cosα+ysinα-p=0【适用于不平行于坐标轴的直线】 过原点向直线做一条的垂线段,该垂线段所在直线的倾斜角为α,p是该线段的长度 高中数学知识点9:点向式:(x-x0)/u=(y-y0)/v (u≠0,v≠0)【适用于任何直线】 表示过点(x0,y0)且方向向量为(u,v )的直线 高中数学知识点10:法向式:a(x-x0)+b(y-y0)=0【适用于任何直线】 表示过点(x0,y0)且与向量(a,b)垂直的直线 文章来源于网络,由编辑整理,如有侵权请及时联系删除。 (责任编辑:admin) |