2018高考数学二轮复习数列知识专题总结
http://www.newdu.com 2025/05/21 03:05:09 三好网 佚名 参加讨论
2018年高考二轮复习是高考成绩提升的关键期,考生一定要积极备考,梳理高中学科知识脉络,牢记知识点。小编整理了2018高考数学二轮复习知识点,数列知识总结如下: 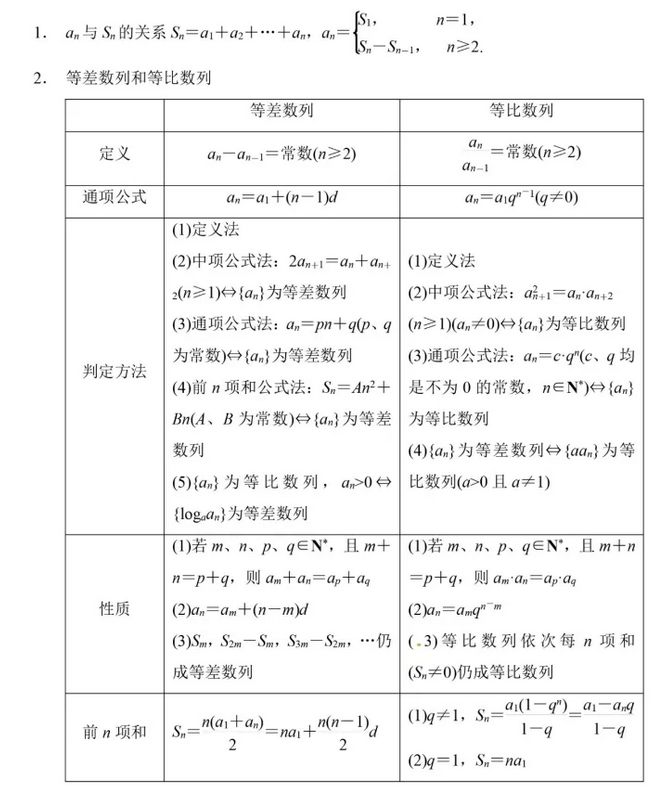 1、如果一个数列是等差数列或等比数列,则求和时直接利用等差、等比数列的前n项和公式,注意等比数列公比q的取值情况要分q=1或q≠1. 2、一些常见数列的前n项和公式: 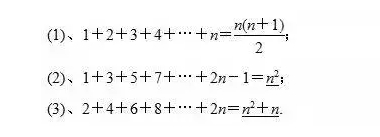  二、非等差、等比数列求和的常用方法 1、倒序相加法 如果一个数列{an},首末两端等“距离”的两项的和相等或等于同一常数,那么求这个数列的前n项和即可用倒序相加法,等差数列的前n项和即是用此法推导的. 2、分组转化求和法 若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组转化法,分别求和而后相加减. 3、错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和即可用此法来求,等比数列的前n项和就是用此法推导的. 4、裂项相消法 把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和.  三、数列求和的方法 1、一般的数列求和,应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为与特殊数列有关或具备某种方法适用特点的形式,从而选择合适的方法求和. 2、解决非等差、等比数列的求和,主要有两种思路: ①转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相减来完成. ②不能转化为等差或等比数列的数列,往往通过裂项相消法、错位相减法、倒序相加法等来求和.  四、分组转化法求和的常见类型   五、用错位相减法求和应注意 1、要善于识别题目类型,特别是等比数列公比为负数的情形; 2、在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式. 3、在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.  六、利用裂项相消法求和应注意   文章来源于网络,由编辑整理,如有侵权请及时联系删除。 (责任编辑:admin) |