2017高一上学期期中考后,二次函数闭区间上最值题解析
http://www.newdu.com 2025/05/21 05:05:41 三好网 佚名 参加讨论
2017高一上学期期中考试,二次函数的区间最值问题,核心是函数对称轴与给定区间的相对位置关系的讨论。一般分为:对称轴在区间的左边,中间,右边三种情况。小编整理出分析方法如下:  例题分析归类: (一)正向型 正向型是指已知二次函数和定义域区间,求其最值. 对称轴与定义域区间的相互位置关系的讨论往往成 为解决这类问题的关键.此类问题包括以下四种情形: (1)轴定,区间定; (2)轴定,区间变; (3)轴变,区间定; (4)轴变,区间变. 1:轴定区间定 二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”.  2:轴定区间变 二次函数是确定的,但它的定义域区间是随参数而变化的,我们称这种情况是“定函数在动区间上的最值”.  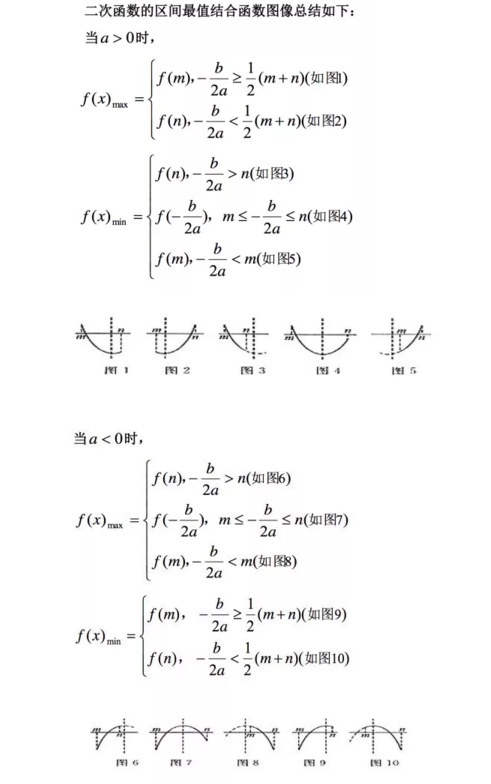 3:轴变区间定 二次函数随着参数的变化而变化,即其图像是运动的,但定义域区间是固定的,我们称这种情况是“动二次函数在定区间上的最值”.  4:轴变区间变 二次函数是含参数的函数,而定义域区间也是变化的,我们称这种情况是“动二次函数在动区间上的最值”.   (二)逆向型 逆向型是指已知二次函数在某区间上的最值,求函数或区间中参数的取值.     (责任编辑:admin) |