2017高考数学政策解读,新大纲修订下的备考策略与权威解读
http://www.newdu.com 2025/05/20 05:05:44 三好网 佚名 参加讨论
2017高考数学政策解读,新大纲修订下的备考策略与权威解读。2017年高考数学考试大纲进行了修订,那高三生如何根据考纲要求抓住高考数学核心考点,掌握适合自己的高中数学解题技巧呢?高考辅导数学专家又将对此数学考纲的调整做何种解读呢?  【修订原因】 从整体看,此次数学高考大纲的修订与新课标的修订有关。大家对新课标的修订都已经有所了解,所以老师和学生应该已经有心理准备了,并不突然。 这次修订的大纲删去了“几何证明选讲”选考模块,这对学生来说影响不会很大,因为从往年高考看,这个模块是选考中的一块,而学生多数都不会选择这个模块。 对于数学文化,其实在近两年的高考试题中已经有所体现,只是今年新修订的大纲更加强调。我国古代数学里有大量的实际问题,可以结合函数、数列、立体几何、算法等内容。这些问题同时也体现了应用性的考查,理应引起考生的充分重视。 【命题预测】 2017年高考数学是从3个选考模块中删掉了一个——“几何证明选讲”。2017届考生们只需要从剩下的“坐标系与参数方程”和“不等式选讲”中二选一作答。不过代价也是要有的,新考纲中增加了一项要求是“数学文化”……看到这4个字的时候,你是否一脸疑惑呢? 不过大家放心,如果要用文言文来出数学题那就太过分了!顶多以后在做数学题的时候有个题目背景。 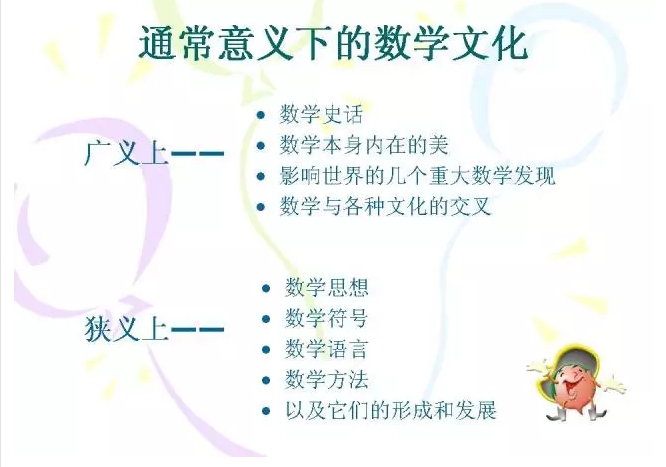 【备考策略】 2017届考生要重视基础知识和基本技能掌握,回归教材,挖掘典型题变式扩展,做到教材上的例题、练习完全过手;要重视思维训练,少搞题海战术,注重书写格式培训,规范表达方式;应该着重抽象思维能力、直观想象能力、逻辑分析能力等方面的训练和提高,不要无目的性地选择大量套题练习,要有意识地选取包含多知识点相融合的题来训练。 听湖南省教科院数学专家谈“数学文化” 数学文化如何在高考命题中体现?我们来听听湖南省教科院数学教研员黄仁寿老师的解读——高考数学命题会这样关注数学的人文价值。 数学文化是数学的一个重要组成部分。数学本身也是一种特殊的文化。从对这种包含关系的认识出发,《2017年全国普通高考考试大纲》中明确指出数学学科的命题要“展现数学的科学价值和人文价值”的要求,也就不难理解了。 数学命题怎样体现数学的人文价值呢(即数学文化题)?下面的题是2015年全国新课标卷的第6题,或许它就是数学文化题的一个范式: 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )  既然是数学文化题也就免不了数学文化题特有的味道。本题题干中的“《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:‘今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?’”就属于这种味道。另外,题目中的度量单位“斛”和匹配的图片也属于数学文化,因为单位“斛”早已退出度量体制,只盛下数学文化的味道了。 那么,是不是数学备考还应训练古汉语翻译呢?从数学备考的角度来说大可不必。此题题干中不是通过“其意思为”对古汉语的意思作了完整的解释吗?因此,高考数学命题关注数学的人文价值的形式,主要表现为创设数学问题的一个人文情境,让人感受到一种数学文化的味道。正确解答这类问题的关键,在于静心领会题目的含义,提炼出题目情境所隐含的数学本质,依数学的规律给出正确的解答即可。 看看老师们的备考建议: 麓山国际实验学校高三理科数学备课组何文娟表示,新修订的大纲对能力立意有所加强,增加了数学文化知识考察。数学回归全国卷对三视图、算法、立体几何和概率统计考察难度有所提升,圆锥曲线和导数大题入手较以前要容易些,中档题增加了,难易程度趋于平缓。这就要求学生回归教材,强化概念的理解和迁移,更注重基础的学习,按主干知识构建知识网络。 南雅中学教务处主任、数学高级教师石向阳认为,此次考纲最大的变化在于对能力要求内涵方面,增加了基础性、综合性、应用性、创新性的要求,增加了数学文化的要求。同时对能力要求进行了加细说明,使能力要求更加明确具体。他预测2017文理科试卷难度与2016全国卷保持稳定。 他强调,在高考试题中渗透数学文化,可以适当引导中学教学的教学,使得更多的教师关注数学文化,研究数学文化,将数学的本质教授给学生。对于数学文化,其实在近两年的高考试题中已经有所体现(如2015年全国1卷文6理6题),只是今年新修订的大纲更加强调。我国古代数学里有大量的实际问题,可以结合函数、数列、立体几何、算法等内容。高考试题会通过创设新的情境、改变设问方式,选取适合的知识内容等多种方法渗透数学文化。这些问题同时也体现了应用性的考查,应引起考生的充分重视。 大纲强调了核心素养考查,所以对于今后的数学复习来说,学生应该着重抽象思维能力、直观想象能力、逻辑分析能力等方面的训练和提高。不要无目的性地选择大量套题练习,要有意识地选取包含多知识点相融合的综合题来训练,在选取训练题方面,可以在老师指导和帮助有效地进行。 中国古代著名数学著作: 《张丘建算经》 《张丘建算经》共有三卷,约成书于公元466~485年间。张丘建,北魏时清河(今山东临清一带)人,生平不详。 其中,最小公倍数的应用、等差数列各元素互求以及“百鸡术”等是其主要成就。“百鸡术”是世界著名的不定方程问题。 《四元玉鉴》 朱世杰(1300前后),字汉卿,号松庭,寓居燕山。数学代表作有《算学启蒙》(1299)和《四元玉鉴》(1303)。 《算学启蒙》是一部通俗数学名著,曾流传海外,影响了朝鲜、日本数学的发展。 《四元玉鉴》则是中国宋元数学高峰的又一个标志,其中最杰出的数学创作有“四元术”(多元高次方程列式与消元解法)、“垛积法”(高阶等差数列求和)与“招差术”(高次内插法) 《黄帝九章算经细草》 贾宪,北宋人,约于1050年左右完成〈〈黄帝九章算经细草〉〉,原书佚失,但其主要内容被杨辉(约13世纪中)著作所抄录,因能传世。 杨辉〈〈详解九章算法〉〉(1261)载有“开方作法本源”图,注明“贾宪用此术”,这就是著名的“贾宪三角”,或称“杨辉三角”。〈〈详解九章算法〉〉同时录有贾宪进行高次幂开方的“增乘开方法”。 《数书九章》 秦九韶(约1202~1261),字道吉,四川安岳人。 秦九韶与李冶、杨辉、朱世杰并称宋元数学四大家。他早年在杭州“访习于太史,又尝从隐君子受数学”,1247年写成著名的《数书九章》。 《数书九章》全书共18卷,81题,分九大类(大衍、天时、田域、测望、赋役、钱谷、营建、军旅、市易)。 其最重要的数学成就——“大衍总数术”(一次同余组解法)与“正负开方术”(高次方程数值解法),使这部宋代算经在中世纪世界数学史上占有突出的地位。 《九章重差图》 刘徽(约公元225年—295年),汉族,山东邹平县人,是中国数学史上一个非常伟大的数学家,他的杰作《九章算术注》和《海岛算经》,是中国最宝贵的数学遗产,除此之外还著有《九章重差图》。 《重差》原为《九章算术注》的第十卷,即后来的《海岛算经》,内容是测量目标物的高和远的计算方法。重差法是测量数学中的重要方法。 (责任编辑:admin) |